Introduction to Machine Learning
Contents
2. Introduction to Machine Learning¶
In this chapter, we’ll briefly review machine learning concepts that will be relevant later. We’ll focus in particular on the problem of prediction, that is, to model some output variable as a function of observed input covariates.
# loading relevant packages
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.pyplot import figure
import seaborn as sns
import random
import math
import statsmodels.formula.api as smf
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import make_scorer
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import KFold
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import Ridge
import statsmodels.api as sm
from scipy.stats import norm
import warnings
from SyncRNG import SyncRNG
warnings.filterwarnings('ignore')
%matplotlib inline
In this section, we will use simulated data. In the next section we’ll load a real dataset.
# Simulating data
# Sample size
n = 500
# Generating covariate X ~ Unif[-4, 4]
x = np.linspace(-4, 4, n) #with linspace we can generate a vector of "n" numbers between a range of numbers
# Generate outcome
# if x < 0:
# y = cos(2*x) + N(0, 1)
# else:
# y = 1-sin(x) + N(0, 1)
random.shuffle(x)
mu = np.where(x<0, np.cos(2*x), 1-np.sin(x))
y = mu + 1*np.random.normal(size=n)
# collecting observations in a data.frame object
data = pd.DataFrame(np.array([x,y]).T, columns=['x','y'])
The following shows how the two variables x and y relate. Note that the relationship is nonlinear.
plt.figure(figsize=(15,6))
sns.scatterplot(x,y, color = 'red', label = 'Data')
sns.lineplot(x,mu, color = 'black', label = "Ground truth E[Y|X=x]")
plt.yticks(np.arange(-4,4,1))
plt.legend()
plt.xlabel("X")
plt.ylabel("Outcome y")
Text(0, 0.5, 'Outcome y')
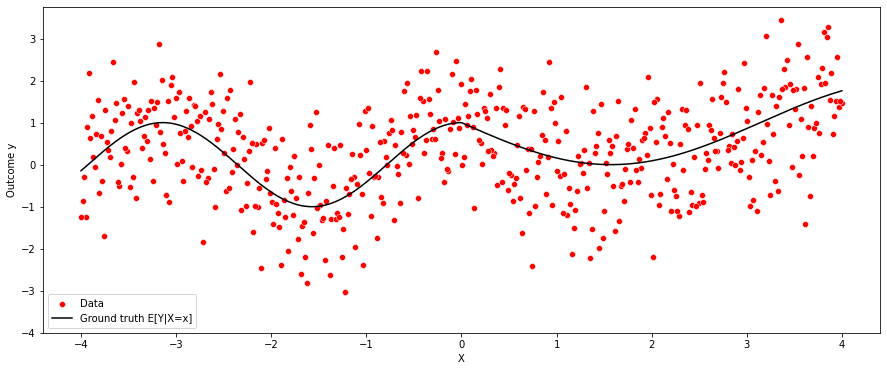
Note: If you’d like to run the code below on a different dataset, you can replace the dataset above with another data.frame of your choice, and redefine the key variable identifiers (outcome, covariates) accordingly. Although we try to make the code as general as possible, you may also need to make a few minor changes to the code below; read the comments carefully.
2.1. Key concepts¶
The prediction problem is to accurately guess the value of some output variable \(Y_i\) from input variables \(X_i\). For example, we might want to predict “house prices given house characteristics such as the number of rooms, age of the building, and so on. The relationship between input and output is modeled in very general terms by some function
where \(\epsilon_i\) represents all that is not captured by information obtained from \(X_i\) via the mapping \(f\). We say that error \(\epsilon_i\) is irreducible.
We highlight that (2.1) is not modeling a causal relationship between inputs and outputs. For an extreme example, consider taking \(Y_i\) to be “distance from the equator” and \(X_i\) to be “average temperature.” We can still think of the problem of guessing (“predicting”) “distance from the equator” given some information about “average temperature,” even though one would expect the former to cause the latter.
In general, we can’t know the “ground truth” \(f\), so we will approximate it from data. Given \(n\) data points \(\{(X_1, Y_1), \cdots, (X_n, Y_n)\}\), our goal is to obtain an estimated model \(\hat{f}\) such that our predictions \(\widehat{Y}_i := \hat{f}(X_i)\) are “close” to the true outcome values \(Y_i\) given some criterion. To formalize this, we’ll follow these three steps:
Modeling: Decide on some suitable class of functions that our estimated model may belong to. In machine learning applications the class of functions can be very large and complex (e.g., deep decision trees, forests, high-dimensional linear models, etc). Also, we must decide on a loss function that serves as our criterion to evaluate the quality of our predictions (e.g., mean-squared error).
Fitting: Find the estimate \(\hat{f}\) that optimizes the loss function chosen in the previous step (e.g., the tree that minimizes the squared deviation between \(\hat{f}(X_i)\) and \(Y_i\) in our data).
Evaluation: Evaluate our fitted model \(\hat{f}\). That is, if we were given a new, yet unseen, input and output pair \((X',Y')\), we’d like to know if \(Y' \approx \hat{f}(X_i)\) by some metric.
For concreteness, let’s work through an example. Let’s say that, given the data simulated above, we’d like to predict \(Y_i\) from the first covariate \(X_{i1}\) only. Also, let’s say that our model class will be polynomials of degree \(q\) in \(X_{i1}\), and we’ll evaluate fit based on mean squared error. That is, \(\hat{f}(X_{i1}) = \hat{b}_0 + X_{i1}\hat{b}_1 + \cdots + X_{i1}^q \hat{b}_q\), where the coefficients are obtained by solving the following problem:
An important question is what is \(q\), the degree of the polynomial. It controls the complexity of the model. One may imagine that more complex models are better, but that is not always true, because a very flexible model may try to simply interpolate over the data at hand, but fail to generalize well for new data points. We call this overfitting. The main feature of overfitting is high variance, in the sense that, if we were given a different data set of the same size, we’d likely get a very different model.
To illustrate, in the figure below we let the degree be \(q=10\) but use only the first few data points. The fitted model is shown in green, and the original data points are in red.
X = data.loc[:,'x'].values.reshape(-1, 1)
Y = data.loc[:,'y'].values.reshape(-1, 1)
# Note: this code assumes that the first covariate is continuous.
# Fitting a flexible model on very little data
# selecting only a few data points
subset = np.arange(0,30)
# formula for a high-dimensional polynomial regression
# y ~ 1 + x1 + x1^2 + x1^3 + .... + x1^q
poly = PolynomialFeatures(degree = 10)
X_poly = poly.fit_transform(X)
# linear regression using only a few observations
poly.fit(X_poly, Y)
lin2 = LinearRegression()
lin2.fit(X_poly[0:30], Y[0:30])
# compute a grid of x1 values we'll use for prediction
x = data['x']
xgrid = np.linspace(min(x),max(x), 1000)
new_data = pd.DataFrame(xgrid, columns=['x'])
# predict
yhat = lin2.predict(poly.fit_transform(new_data))
# Visualising the Polynomial Regression results
# Plotting observations (in red) and model predictions (in green
plt.figure(figsize=(18,6))
sns.scatterplot(data.loc[subset,'x'],data.loc[subset,'y'], color = 'red', label = 'Data')
plt.plot(xgrid, yhat, color = 'green', label = 'Estimate')
plt.title('Example of overfitting')
plt.xlabel('X')
plt.ylabel('Outcome y')
Text(0, 0.5, 'Outcome y')
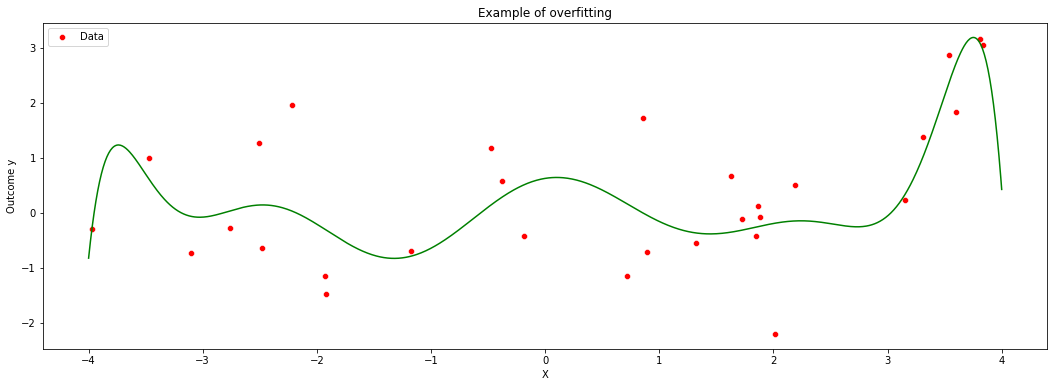
On the other hand, when \(q\) is too small relative to our data, we permit only very simple models and may suffer from misspecification bias. We call this underfitting. The main feature of underfitting is high bias – the selected model just isn’t complex enough to accurately capture the relationship between input and output variables.
To illustrate underfitting, in the figure below we set \(q=1\) (a linear fit).
# Note: this code assumes that the first covariate is continuous
# Fitting a very simply model on very little data
# formula for a linear regression (without taking polynomials of x1)
# y ~ 1 + x1
lin = LinearRegression()
lin.fit(X[0:30], Y[0:30])
# compute a grid of x1 values we'll use for prediction
x = data['x']
xgrid = np.linspace(min(x),max(x), 1000)
new_data = pd.DataFrame(xgrid, columns=['x'])
# predict
yhat = lin.predict(new_data)
# plotting observations (in red) and model predictions (in green)
plt.figure(figsize=(18,6))
sns.scatterplot(data.loc[subset,'x'],data.loc[subset,'y'], color = 'red', label = 'Data')
plt.plot(xgrid, yhat, color = 'green',label = 'Estimate')
plt.title('Example of underfitting')
plt.xlabel('X')
plt.ylabel('Outcome y')
Text(0, 0.5, 'Outcome y')
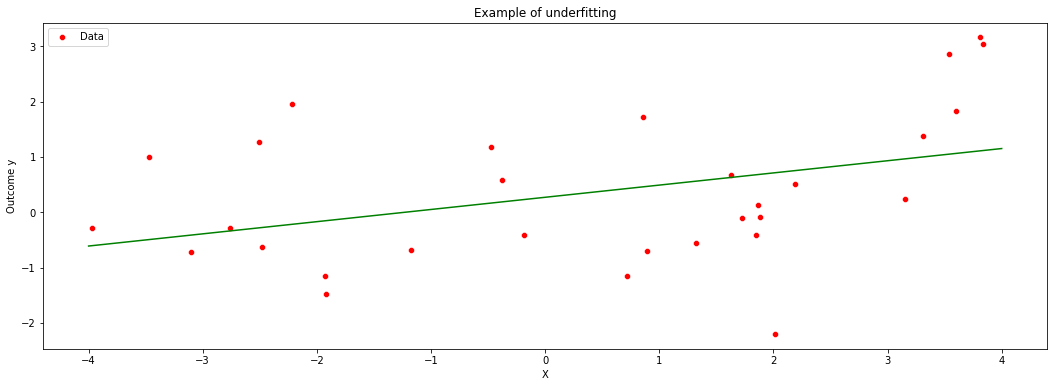
This tension is called the bias-variance trade-off: simpler models underfit and have more bias, more complex models overfit and have more variance.
One data-driven way of deciding an appropriate level of complexity is to divide the available data into a training set (where the model is fit) and the validation set (where the model is evaluated). The next snippet of code uses the first half of the data to fit a polynomial of order \(q\), and then evaluates that polynomial on the second half. The training MSE estimate decreases monotonically with the polynomial degree, because the model is better able to fit on the training data; the test MSE estimate starts increasing after a while reflecting that the model no longer generalizes well.
# polynomial degrees that we'll loop over
degrees =np.arange(3, 21)
# training data observations: 1 to (n/2)
train_mse =[]
test_mse =[]
# looping over each polynomial degree
for d in degrees:
# formula y ~ 1 + x1 + x1^2 + ... + x1^q
# linear regression using the formula above
# note we're fitting only on the training data observations
poly = PolynomialFeatures(degree = d, include_bias =False )
poly_features = poly.fit_transform(X)
# predicting on the training subset
# (no need to pass a dataframe)
X_train, X_test, y_train, y_test = train_test_split(poly_features,y, train_size=0.5 , random_state= 0)
# Now since we want the valid and test size to be equal (10% each of overall data).
# we have to define valid_size=0.5 (that is 50% of remaining data)
poly_reg_model = LinearRegression()
poly_reg_model.fit(X_train, y_train)
# predicting on the validation subset
# (the minus sign in "-train" excludes observations in the training data)
y_train_pred = poly_reg_model.predict(X_train)
y_test_pred = poly_reg_model.predict(X_test)
# compute the mse estimate on the validation subset and output it
mse_train= mean_squared_error(y_train, y_train_pred)
mse_test= mean_squared_error(y_test, y_test_pred)
train_mse.append(mse_train)
test_mse.append(mse_test)
fig, ax = plt.subplots(figsize=(14,6))
ax.plot(degrees, train_mse,color ="black", label = "Training")
ax.plot(degrees, test_mse,"r--", label = "Validation")
ax.set_title("MSE Estimates (train test split)", fontsize =14)
ax.set(xlabel = "Polynomial degree", ylabel = "MSE estimate")
ax.annotate("Low bias \n High Variance", xy=(16, 1.23), xycoords='data', xytext=(14, 1.23), textcoords='data',
arrowprops=dict(arrowstyle="->",connectionstyle="arc3"),)
ax.annotate("High bias \n Low Variance", xy=(5.3, 1.30), xycoords='data', xytext=(7, 1.30), textcoords='data',
arrowprops=dict(arrowstyle="->",connectionstyle="arc3"),)
Text(7, 1.3, 'High bias \n Low Variance')
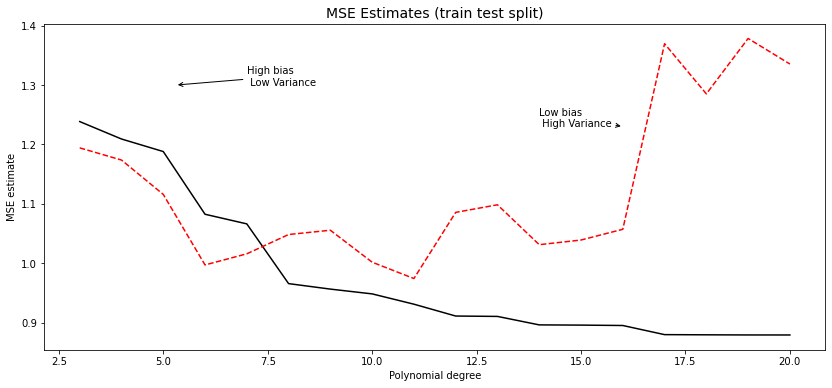
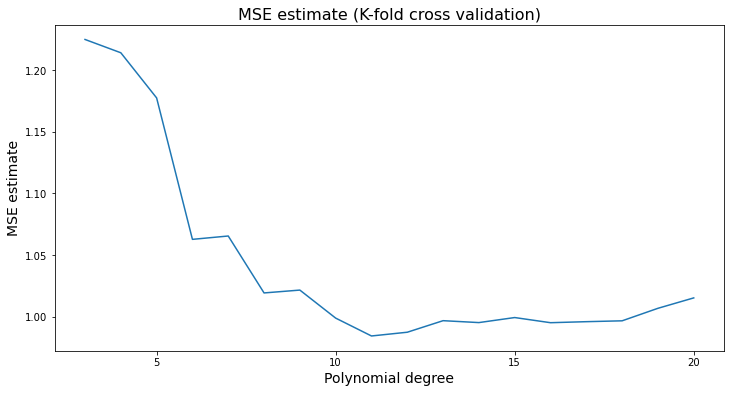
To make better use of the data we will often divide the data into \(K\) subsets, or folds. Then one fits \(K\) models, each using \(K-1\) folds and then evaluation the fitted model on the remaining fold. This is called k-fold cross-validation.
#cv = KFold(n_splits=10, random_state=1, shuffle=True)
scorer = make_scorer
mse =[]
# looping over polynomial degrees (q)
for d in degrees:
# formula y ~ 1 + x1 + x1^2 + ... + x1^q
# polynomial degrees that we'll loop over to select
poly = PolynomialFeatures(degree = d, include_bias =False )
poly_features = poly.fit_transform(X)
# fit on K-1 folds, leaving out observations in fold.idx
# (the minus sign in -fold.idx excludes those observations)
ols = LinearRegression()
# cross-validated mse estimate
scorer = make_scorer(mean_squared_error)
mse_test = cross_val_score(ols, poly_features, y, scoring=scorer, cv =5).mean()
mse.append(mse_test)
# plot
plt.figure(figsize=(12,6))
plt.plot(degrees, mse)
plt.xlabel('Polynomial degree', fontsize = 14)
plt.xticks(np.arange(5,21,5))
plt.ylabel('MSE estimate', fontsize = 14)
plt.title('MSE estimate (K-fold cross validation)', fontsize =16)
#different to r, the models in python got a better performance with more training cause by the
#cross validation and the kfold
Text(0.5, 1.0, 'MSE estimate (K-fold cross validation)')
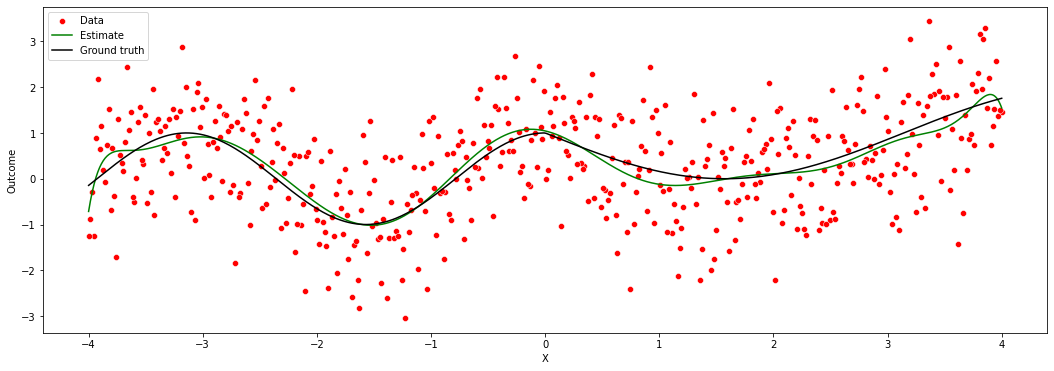
A final remark is that, in machine learning applications, the complexity of the model often is allowed to increase with the available data. In the example above, even though we weren’t very successful when fitting a high-dimensional model on very little data, if we had much more data perhaps such a model would be appropriate. The next figure again fits a high order polynomial model, but this time on many data points. Note how, at least in data-rich regions, the model is much better behaved, and tracks the average outcome reasonably well without trying to interpolate wildly of the data points.
# Note this code assumes that the first covariate is continuous
# Fitting a flexible model on a lot of data
# now using much more data
subset = np.arange(0,500)
X = data.loc[:,'x'].values.reshape(-1, 1)
Y = data.loc[:,'y'].values.reshape(-1, 1)
# formula for high order polynomial regression
# y ~ 1 + x1 + x1^2 + ... + x1^q
poly = PolynomialFeatures(degree = 15)
# linear regression
X_poly = poly.fit_transform(X)
poly.fit(X_poly, Y)
lin2 = LinearRegression()
lin2.fit(X_poly[0:500], Y[0:500])
# compute a grid of x1 values we'll use for prediction
x = data['x']
xgrid = np.linspace(min(x),max(x), 1000)
new_data = pd.DataFrame(xgrid, columns=['x'])
# predict
yhat = lin2.predict(poly.fit_transform(new_data))
# Visualising the Polynomial Regression results
# plotting observations (in red) and model predictions (in green)
plt.figure(figsize=(18,6))
sns.scatterplot(data.loc[subset,'x'],data.loc[subset,'y'], color = 'red', label = 'Data')
plt.plot(xgrid, yhat, color = 'green', label = 'Estimate')
sns.lineplot(x,mu, color = 'black', label = "Ground truth")
plt.xlabel('X')
plt.ylabel('Outcome')
Text(0, 0.5, 'Outcome')
This is one of the benefits of using machine learning-based models: more data implies more flexible modeling, and therefore potentially better predictive power – provided that we carefully avoid overfitting.
The example above based on polynomial regression was used mostly for illustration. In practice, there are often better-performing algorithms. We’ll see some of them next.
2.2. Common machine learning algorithms¶
Next, we’ll introduce three machine learning algorithms: (regularized) linear models, trees, and forests. Although this isn’t an exhaustive list, these algorithms are common enough that every machine learning practitioner should know about them. They also have convenient R packages that allow for easy coding.
In this tutorial, we’ll focus heavily on how to interpret the output of machine learning models – or, at least, how not to mis-interpret it. However, in this chapter we won’t be making any causal claims about the relationships between variables yet. But please hang tight, as estimating causal effects will be one of the main topics presented in the next chapters.
For the remainder of the chapter we will use a real dataset. Each row in this data set represents the characteristics of a owner-occupied housing unit. Our goal is to predict the (log) price of the housing unit (LOGVALUE, our outcome variable) from features such as the size of the lot (LOT) and square feet area (UNITSF), number of bedrooms (BEDRMS) and bathrooms (BATHS), year in which it was built (BUILT) etc. This dataset comes from the American Housing Survey and was used in Mullainathan and Spiess (2017, JEP). In addition, we will append to this data columns that are pure noise. Ideally, our fitted model should not take them into acccount.
import requests
import io
# load dataset
url = 'https://docs.google.com/uc?id=1qHr-6nN7pCbU8JUtbRDtMzUKqS9ZlZcR&export=download'
urlData = requests.get(url).content
data = pd.read_csv(io.StringIO(urlData.decode('utf-8')))
data.drop(['Unnamed: 0'], axis=1, inplace=True)
# outcome variable name
outcome = 'LOGVALUE'
# covariates
true_covariates = ['LOT','UNITSF','BUILT','BATHS','BEDRMS','DINING','METRO','CRACKS','REGION','METRO3','PHONE','KITCHEN','MOBILTYP','WINTEROVEN','WINTERKESP','WINTERELSP','WINTERWOOD','WINTERNONE','NEWC','DISH','WASH','DRY','NUNIT2','BURNER','COOK','OVEN','REFR','DENS','FAMRM','HALFB','KITCH','LIVING','OTHFN','RECRM','CLIMB','ELEV','DIRAC','PORCH','AIRSYS','WELL','WELDUS','STEAM','OARSYS']
p_true = len(true_covariates)
# noise covariates added for didactic reasons
p_noise = 20
noise_covariates = []
for x in range(1, p_noise+1):
noise_covariates.append('noise{0}'.format(x))
covariates = true_covariates + noise_covariates
x_noise = np.random.rand(data.shape[0] * p_noise).reshape(28727,20)
x_noise = pd.DataFrame(x_noise, columns=noise_covariates)
data = pd.concat([data, x_noise], axis=1)
# sample size
n = data.shape[0]
# total number of covariates
p = len(covariates)
Here’s the correlation between the first few covariates. Note how, most variables are positively correlated, which is expected since houses with more bedrooms will usually also have more bathrooms, larger area, etc.
data.loc[:,covariates[0:8]].corr()
| LOT | UNITSF | BUILT | BATHS | BEDRMS | DINING | METRO | CRACKS | |
|---|---|---|---|---|---|---|---|---|
| LOT | 1.000000 | 0.064841 | 0.044639 | 0.057325 | 0.009626 | -0.015348 | 0.136258 | 0.016851 |
| UNITSF | 0.064841 | 1.000000 | 0.143201 | 0.428723 | 0.361165 | 0.214030 | 0.057441 | 0.033548 |
| BUILT | 0.044639 | 0.143201 | 1.000000 | 0.434519 | 0.215109 | 0.037468 | 0.323703 | 0.092390 |
| BATHS | 0.057325 | 0.428723 | 0.434519 | 1.000000 | 0.540230 | 0.259457 | 0.189812 | 0.062819 |
| BEDRMS | 0.009626 | 0.361165 | 0.215109 | 0.540230 | 1.000000 | 0.281846 | 0.121331 | 0.026779 |
| DINING | -0.015348 | 0.214030 | 0.037468 | 0.259457 | 0.281846 | 1.000000 | 0.022026 | 0.021270 |
| METRO | 0.136258 | 0.057441 | 0.323703 | 0.189812 | 0.121331 | 0.022026 | 1.000000 | 0.057545 |
| CRACKS | 0.016851 | 0.033548 | 0.092390 | 0.062819 | 0.026779 | 0.021270 | 0.057545 | 1.000000 |
2.2.1. Generalized linear models¶
This class of models extends common methods such as linear and logistic regression by adding a penalty to the magnitude of the coefficients. Lasso penalizes the absolute value of slope coefficients. For regression problems, it becomes
Similarly, in a regression problem Ridge penalizes the sum of squares of the slope coefficients,
Also, there exists the Elastic Net penalization which consists of a convex combination between the other two. In all cases, the scalar parameter \(\lambda\) controls the complexity of the model. For \(\lambda=0\), the problem reduces to the “usual” linear regression. As \(\lambda\) increases, we favor simpler models. As we’ll see below, the optimal parameter \(\lambda\) is selected via cross-validation.
An important feature of Lasso-type penalization is that it promotes sparsity – that is, it forces many coefficients to be exactly zero. This is different from Ridge-type penalization, which forces coefficients to be small.
Another interesting property of these models is that, even though they are called “linear” models, this should actually be understood as linear in transformations of the covariates. For example, we could use polynomials or splines (continuous piecewise polynomials) of the covariates and allow for much more flexible models.
In fact, because of the penalization term, problems (2.2) and (2.3) remain well-defined and have a unique solution even in high-dimensional problems in which the number of coefficients \(p\) is larger than the sample size \(n\) – that is, our data is “fat” with more columns than rows. These situations can arise either naturally (e.g. genomics problems in which we have hundreds of thousands of gene expression information for a few individuals) or because we are including many transformations of a smaller set of covariates.
Finally, although here we are focusing on regression problems, other generalized linear models such as logistic regression can also be similarly modified by adding a Lasso, Ridge, or Elastic Net-type penalty to similar consequences.
X = data.loc[:,covariates]
Y = data.loc[:,outcome]
from sklearn.linear_model import Lasso
# A formula of type "~ x1 + x2 + ..." (right-hand side only) to
# indicate how covariates should enter the model. If you'd like to add, e.g.,
# third-order polynomials in x1, you could do so here by modifying the formula
# to be something like "~ poly(x1, 3) + x2 + ..."
lasso = Lasso()
alphas = np.logspace(np.log10(1e-8), np.log10(1e-1), 100)
tuned_parameters = [{"alpha": alphas}]
n_folds = 10
scorer = make_scorer(mean_squared_error)
# Use this formula instead if you'd like to fit on piecewise polynomials
# fmla <- formula(paste(" ~ 0 + ", paste0("bs(", covariates, ", df=5)", collapse=" + ")))
# Function model.matrix selects the covariates according to the formula
# above and expands the covariates accordingly. In addition, if any column
# is a factor, then this creates dummies (one-hot encoding) as well.
clf = GridSearchCV(lasso, tuned_parameters, cv=n_folds, refit=False, scoring=scorer)
# Fit a lasso model.
# Note this automatically performs cross-validation.
clf.fit(X, Y)
scores = clf.cv_results_["mean_test_score"]
scores_std = clf.cv_results_["std_test_score"]
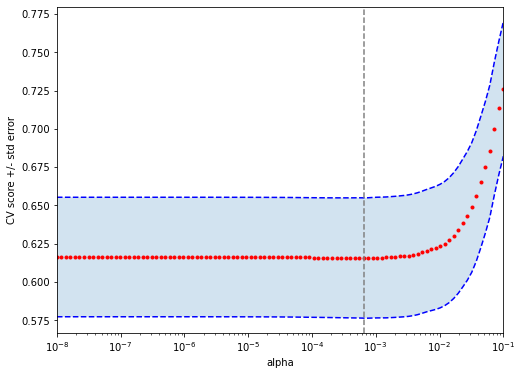
The next figure plots the average estimated MSE for each lambda. The red dots are the averages across all folds, and the error bars are based on the variability of mse estimates across folds. The vertical dashed lines show the (log) lambda with smallest estimated MSE (left) and the one whose mse is at most one standard error from the first (right).
data_lasso = pd.DataFrame([pd.Series(alphas, name= "alphas"), pd.Series(scores, name = "scores")]).T
best = data_lasso[data_lasso["scores"] == np.min(data_lasso["scores"])]
plt.figure().set_size_inches(8, 6)
plt.semilogx(alphas, scores, ".", color = "red")
# plot error lines showing +/- std. errors of the scores
std_error = scores_std / np.sqrt(n_folds)
plt.semilogx(alphas, scores + std_error, "b--")
plt.semilogx(alphas, scores - std_error, "b--")
# alpha=0.2 controls the translucency of the fill color
plt.fill_between(alphas, scores + std_error, scores - std_error, alpha=0.2)
plt.ylabel("CV score +/- std error")
plt.xlabel("alpha")
plt.axvline(best.iloc[0,0], linestyle="--", color=".5")
plt.xlim([alphas[0], alphas[-1]])
(1e-08, 0.1)
Here are the first few estimated coefficients at the \(\lambda\) value that minimizes cross-validated MSE. Note that many estimated coefficients them are exactly zero.
# Estimated coefficients at the lambda value that minimized cross-validated MSE
lasso = Lasso(alpha=best.iloc[0,0])
lasso.fit(X,Y)
table = np.zeros((1,5))
table[0,0] = lasso.intercept_
table[0,1] = lasso.coef_[0]
table[0,2] = lasso.coef_[1]
table[0,3] = lasso.coef_[2]
table[0,4] = lasso.coef_[3]
pd.DataFrame(table, columns=['(Intercept)','LOT','UNITSF','BUILT','BATHS'], index=['Coef.']) # showing only first coefficients
| (Intercept) | LOT | UNITSF | BUILT | BATHS | |
|---|---|---|---|---|---|
| Coef. | 11.643421 | 3.494443e-07 | 0.000023 | 0.000229 | 0.246402 |
print("Number of nonzero coefficients at optimal lambda:", len(lasso.coef_[lasso.coef_ != 0]), "out of " , len(lasso.coef_))
Number of nonzero coefficients at optimal lambda: 46 out of 63
Predictions and estimated MSE for the selected model are retrieved as follows.
# Retrieve predictions at best lambda regularization parameter
y_hat = lasso.predict(X)
# Get k-fold cross validation
mse_lasso = best.iloc[0,1]
print("glmnet MSE estimate (k-fold cross-validation):", mse_lasso)
glmnet MSE estimate (k-fold cross-validation): 0.6156670911339063
The next command plots estimated coefficients as a function of the regularization parameter \(\lambda\).
coefs = []
for a in alphas:
lasso.set_params(alpha=a)
lasso.fit(X, Y)
coefs.append(lasso.coef_)
plt.figure(figsize=(18,6))
plt.gca().plot(alphas, coefs)
plt.gca().set_xscale('log')
plt.axis('tight')
plt.xlabel('alpha')
plt.ylabel('Standardized Coefficients')
plt.title('Lasso coefficients as a function of alpha');
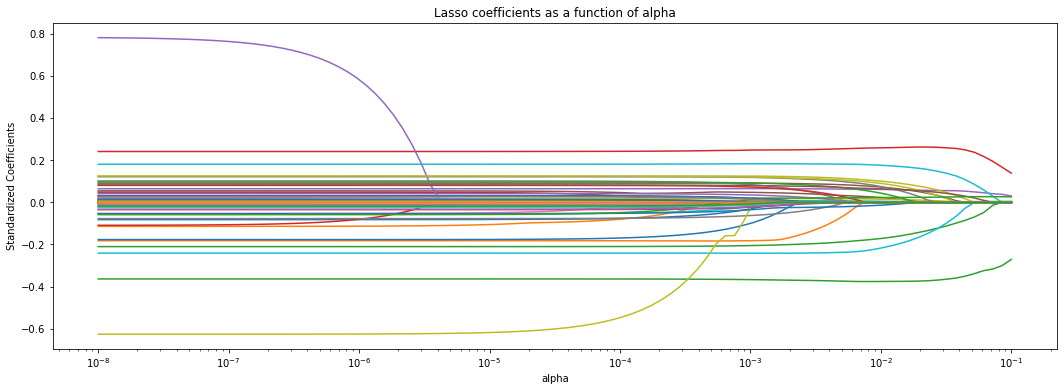
It’s tempting to try to interpret the coefficients obtained via Lasso. Unfortunately, that can be very difficult, because by dropping covariates Lasso introduces a form of omitted variable bias (wikipedia). To understand this form of bias, consider the following toy example. We have two positively correlated independent variables, x.1 and x.2, that are linearly related to the outcome y. Linear regression of y on x1 and x2 gives us the correct coefficients. However, if we omit x2 from the estimation model, the coefficient on x1 increases. This is because x1 is now “picking up” the effect of the variable that was left out. In other words, the effect of x1 seems stronger because we aren’t controlling for some other confounding variable. Note that the second model this still works for prediction, but we cannot interpret the coefficient as a measure of strength of the causal relationship between x1 and y.
# Generating some data
# y = 1 + 2*x1 + 3*x2 + noise, where corr(x1, x2) = .5
# note the sample size is very large -- this isn't solved by big data!
mean = [0.0,0.0]
cov = [[1.5,1],[1,1.5]]
x1, x2 = np.random.multivariate_normal(mean, cov, 100000).T
y = 1 + 2*x1 + 3*x2 + np.random.rand(100000)
data_sim = pd.DataFrame(np.array([x1,x2,y]).T,columns=['x1','x2','y'] )
print('Correct Model')
Correct Model
result = smf.ols('y ~ x1 + x2', data = data_sim).fit()
print(result.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.997
Model: OLS Adj. R-squared: 0.997
Method: Least Squares F-statistic: 1.897e+07
Date: Wed, 22 Jun 2022 Prob (F-statistic): 0.00
Time: 20:59:12 Log-Likelihood: -17706.
No. Observations: 100000 AIC: 3.542e+04
Df Residuals: 99997 BIC: 3.545e+04
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 1.5012 0.001 1643.500 0.000 1.499 1.503
x1 1.9998 0.001 1996.643 0.000 1.998 2.002
x2 3.0011 0.001 3002.007 0.000 2.999 3.003
==============================================================================
Omnibus: 90005.976 Durbin-Watson: 2.010
Prob(Omnibus): 0.000 Jarque-Bera (JB): 6016.746
Skew: -0.006 Prob(JB): 0.00
Kurtosis: 1.798 Cond. No. 2.24
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
print("Model with omitted variable bias")
result = smf.ols('y ~ x1', data = data_sim).fit()
print(result.summary())
Model with omitted variable bias
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.760
Model: OLS Adj. R-squared: 0.760
Method: Least Squares F-statistic: 3.174e+05
Date: Wed, 22 Jun 2022 Prob (F-statistic): 0.00
Time: 20:59:21 Log-Likelihood: -2.4332e+05
No. Observations: 100000 AIC: 4.866e+05
Df Residuals: 99998 BIC: 4.867e+05
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 1.5107 0.009 173.262 0.000 1.494 1.528
x1 4.0084 0.007 563.401 0.000 3.994 4.022
==============================================================================
Omnibus: 0.159 Durbin-Watson: 2.003
Prob(Omnibus): 0.924 Jarque-Bera (JB): 0.158
Skew: -0.003 Prob(JB): 0.924
Kurtosis: 3.001 Cond. No. 1.23
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
The phenomenon above occurs in Lasso and in any other sparsity-promoting method when correlated covariates are present since, by forcing coefficients to be zero, Lasso is effectively dropping them from the model. And as we have seen, as a variable gets dropped, a different variable that is correlated with it can “pick up” its effect, which in turn can cause bias. Once \(\lambda\) grows sufficiently large, the penalization term overwhelms any benefit of having that variable in the model, so that variable finally decreases to zero too.
One may instead consider using Lasso to select a subset of variables, and then regressing the outcome on the subset of selected variables via OLS (without any penalization). This method is often called post-lasso. Although it has desirable properties in terms of model fit (see e.g., Belloni and Chernozhukov, 2013), this procedure does not solve the omitted variable issue we mentioned above.
We illustrate this next. We observe the path of the estimated coefficient on the number of bathroooms (BATHS) as we increase \(\lambda\).
# prepare data
scale_X = StandardScaler().fit(X).transform(X)
###############################################
# fit ols model
ols = LinearRegression()
ols.fit(scale_X,Y)
ols_coef = ols.coef_[3]
lamdas = np.linspace(0.01,0.4, 100)
# retrieve ols coefficients
coef_ols = np.repeat(ols_coef,100)
###############################################
# fit lasso model
lasso_bath_coef = []
# retrieve lasso coefficients
lasso_coefs=[]
for a in lamdas:
lasso.set_params(alpha=a,normalize = False)
lasso.fit(scale_X, Y)
lasso_bath_coef.append(lasso.coef_[3])
lasso_coefs.append(lasso.coef_)
#################################################
# fit ridge model
ridge_bath_coef = []
# retrieve ridge coefficients
for a in lamdas:
ridge = Ridge(alpha=a,normalize = True)
ridge.fit(scale_X, Y)
ridge_bath_coef.append(ridge.coef_[3])
####################################################
# fit post-lasso model
poslasso_coef = [ ]
#loop over lasso coefficients and re-fit OLS to get post-lasso coefficients
for a in range(100):
# which slopes are non-zero
scale_X = StandardScaler().fit(X.iloc[:, (lasso_coefs[a] != 0)]).transform(X.iloc[:, (lasso_coefs[a] != 0)])
# if there are any non zero coefficients, estimate OLS
ols = LinearRegression()
ols.fit(scale_X,Y)
# populate post-lasso coefficients
post_coef = ols.coef_[X.iloc[:, (lasso_coefs[a] != 0)].columns.get_loc('BATHS')]
poslasso_coef.append(post_coef )
#################################################
plt.figure(figsize=(18,5))
plt.plot(lamdas, ridge_bath_coef, label = 'Ridge', color = 'g', marker='+', linestyle = ':',markevery=8)
plt.plot(lamdas, lasso_bath_coef, label = 'Lasso', color = 'r', marker = '^',linestyle = 'dashed',markevery=8)
plt.plot(lamdas, coef_ols, label = 'OLS', color = 'b',marker = 'x',linestyle = 'dashed',markevery=8)
plt.plot(lamdas, poslasso_coef, label = 'postlasso',color='black',marker = 'o',linestyle = 'dashed',markevery=8 )
plt.legend()
plt.title("Coefficient estimate on Baths")
plt.ylabel('Coef')
plt.xlabel('lambda')
Text(0.5, 0, 'lambda')
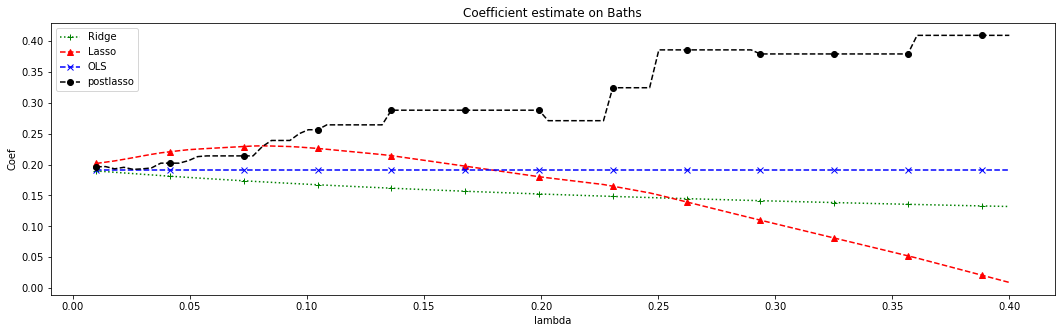
The OLS coefficients are not penalized, so they remain constant. Ridge estimates decrease monotonically as \(\lambda\) grows. Also, for this dataset, Lasso estimates first increase and then decrease. Meanwhile, the post-lasso coefficient estimates seem to behave somewhat erratically with \(lambda\). To understand this behavior, let’s see what happens to the magnitude of other selected variables that are correlated with BATHS.
scale_X = StandardScaler().fit(X).transform(X)
UNITSF_coef = []
BEDRMS_coef = []
DINING_coef = []
for a in lamdas:
lasso.set_params(alpha=a,normalize = False)
lasso.fit(scale_X, Y)
UNITSF_coef.append(lasso.coef_[1])
BEDRMS_coef.append(lasso.coef_[4])
DINING_coef.append(lasso.coef_[5])
plt.figure(figsize=(18,5))
plt.plot(lamdas, UNITSF_coef,label = 'UNITSF', color = 'black' )
plt.plot(lamdas, BEDRMS_coef,label = 'BEDRMS', color = 'red', linestyle = '--')
plt.plot(lamdas, DINING_coef,label = 'DINING', color = 'g',linestyle = 'dotted')
plt.legend()
plt.ylabel('Coef')
plt.xlabel('lambda')
Text(0.5, 0, 'lambda')
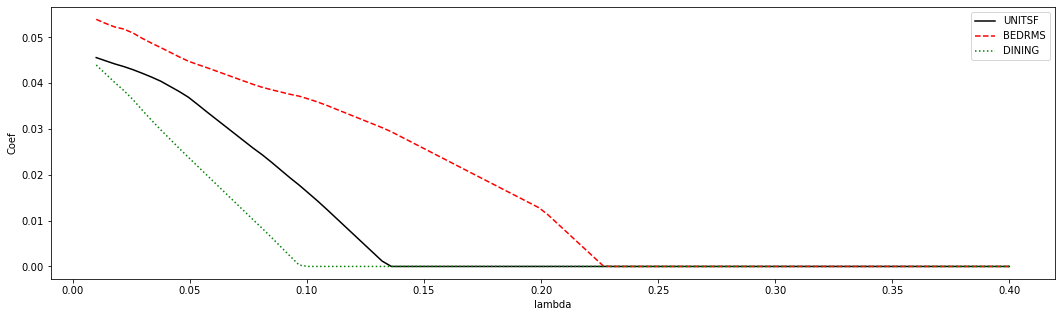
Note how the discrete jumps in magnitude for the BATHS coefficient in the first coincide with, for example, variables DINING and BEDRMS being exactly zero. As these variables got dropped from the model, the coefficient on BATHS increased to pick up their effect.
Another problem with Lasso coefficients is their instability. When multiple variables are highly correlated we may spuriously drop several of them. To get a sense of the amount of variability, in the next snippet we fix \(\lambda\) and then look at the lasso coefficients estimated during cross-validation. We see that by simply removing one fold we can get a very different set of coefficients (nonzero coefficients are in black in the heatmap below). This is because there may be many choices of coefficients with similar predictive power, so the set of nonzero coefficients we end up with can be quite unstable.
import itertools
# Fixing lambda. This choice is not very important; the same occurs any intermediate lambda value.
nobs = X.shape[0]
nfold = 10
# Define folds indices
list_1 = [*range(0, nfold, 1)]*nobs
sample = np.random.choice(nobs,nobs, replace=False).tolist()
foldid = [list_1[index] for index in sample]
# Create split function(similar to R)
def split(x, f):
count = max(f) + 1
return tuple( list(itertools.compress(x, (el == i for el in f))) for i in range(count) )
# Split observation indices into folds
list_2 = [*range(0, nobs, 1)]
I = split(list_2, foldid)
from sklearn.linear_model import LassoCV
scale_X = StandardScaler().fit(X).transform(X)
lasso_coef_fold=[]
for b in range(0,len(I)):
# Split data - index to keep are in mask as booleans
include_idx = set(I[b]) #Here should go I[b] Set is more efficient, but doesn't reorder your elements if that is desireable
mask = np.array([(i in include_idx) for i in range(len(X))])
# Lasso regression, excluding folds selected
lassocv = LassoCV(random_state=0)
lassocv.fit(scale_X[~mask], Y[~mask])
lasso_coef_fold.append(lassocv.coef_)
index_val = ['Fold-1','Fold-2','Fold-3','Fold-4','Fold-5','Fold-6','Fold-7','Fold-8','Fold-9','Fold-10']
df = pd.DataFrame(data= lasso_coef_fold, columns=X.columns, index = index_val).T
df.style.applymap(lambda x: "background-color: white" if x==0 else "background-color: black")
| Fold-1 | Fold-2 | Fold-3 | Fold-4 | Fold-5 | Fold-6 | Fold-7 | Fold-8 | Fold-9 | Fold-10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| LOT | 0.041050 | 0.040789 | 0.039105 | 0.037300 | 0.041148 | 0.043150 | 0.037104 | 0.035392 | 0.037300 | 0.037464 |
| UNITSF | 0.044746 | 0.046055 | 0.047095 | 0.045291 | 0.049540 | 0.043839 | 0.043077 | 0.051535 | 0.047132 | 0.046415 |
| BUILT | 0.001111 | 0.004845 | 0.003385 | 0.003564 | 0.004757 | 0.003220 | 0.003449 | 0.002987 | 0.000929 | 0.004401 |
| BATHS | 0.200578 | 0.189623 | 0.195828 | 0.200489 | 0.192490 | 0.198082 | 0.203624 | 0.200081 | 0.198007 | 0.198827 |
| BEDRMS | 0.055605 | 0.057472 | 0.055982 | 0.055394 | 0.054981 | 0.056335 | 0.054475 | 0.049082 | 0.055994 | 0.052763 |
| DINING | 0.047736 | 0.046748 | 0.047269 | 0.044850 | 0.044751 | 0.046515 | 0.044934 | 0.048129 | 0.046415 | 0.046481 |
| METRO | 0.000000 | 0.000356 | 0.000000 | 0.001081 | 0.001190 | 0.000881 | 0.000000 | 0.003189 | 0.001222 | 0.002415 |
| CRACKS | 0.020332 | 0.020937 | 0.017848 | 0.015932 | 0.019917 | 0.019677 | 0.018395 | 0.023793 | 0.020314 | 0.019614 |
| REGION | 0.083864 | 0.083337 | 0.080464 | 0.081884 | 0.081064 | 0.082150 | 0.078420 | 0.082237 | 0.082466 | 0.082625 |
| METRO3 | 0.007152 | 0.006738 | 0.009395 | 0.009017 | 0.010476 | 0.010692 | 0.007217 | 0.008143 | 0.008373 | 0.007819 |
| PHONE | 0.003223 | 0.004145 | 0.000000 | 0.000000 | 0.003644 | 0.001984 | 0.001331 | 0.003200 | 0.001796 | 0.001127 |
| KITCHEN | -0.003205 | -0.000000 | -0.000955 | -0.002583 | -0.007191 | -0.002836 | -0.000000 | -0.003221 | -0.005402 | -0.000577 |
| MOBILTYP | -0.119085 | -0.103709 | -0.118946 | -0.111606 | -0.106277 | -0.113575 | -0.109086 | -0.103446 | -0.114251 | -0.115418 |
| WINTEROVEN | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| WINTERKESP | 0.000000 | -0.000000 | 0.000000 | 0.000000 | -0.000000 | 0.000000 | 0.000000 | -0.000000 | 0.000000 | 0.000000 |
| WINTERELSP | 0.026793 | 0.021703 | 0.025619 | 0.026638 | 0.026866 | 0.024999 | 0.024933 | 0.030121 | 0.026697 | 0.027365 |
| WINTERWOOD | 0.000000 | -0.000000 | 0.000000 | 0.000000 | -0.000000 | 0.000000 | 0.000000 | -0.000000 | 0.000000 | 0.000000 |
| WINTERNONE | -0.006475 | -0.007696 | -0.001862 | -0.000594 | -0.003744 | -0.001674 | -0.002170 | -0.004903 | -0.008437 | -0.001137 |
| NEWC | 0.029223 | 0.027175 | 0.027914 | 0.026626 | 0.027992 | 0.029549 | 0.031211 | 0.027483 | 0.028221 | 0.028651 |
| DISH | -0.096273 | -0.098615 | -0.095563 | -0.093536 | -0.095071 | -0.097641 | -0.094371 | -0.098233 | -0.095227 | -0.096898 |
| WASH | -0.001606 | -0.008013 | -0.012339 | -0.002369 | -0.016570 | -0.002033 | -0.011885 | -0.004852 | -0.007794 | -0.010408 |
| DRY | -0.034784 | -0.032210 | -0.029772 | -0.031367 | -0.027754 | -0.035728 | -0.029114 | -0.029364 | -0.032434 | -0.026725 |
| NUNIT2 | -0.216673 | -0.229393 | -0.213668 | -0.219420 | -0.230576 | -0.219189 | -0.224386 | -0.228164 | -0.217753 | -0.218393 |
| BURNER | -0.000000 | -0.000000 | 0.000000 | -0.000000 | -0.000000 | -0.000000 | -0.000000 | 0.000000 | 0.000000 | 0.000000 |
| COOK | -0.000000 | -0.000000 | 0.000000 | -0.000000 | -0.000000 | -0.000000 | -0.000000 | 0.000000 | 0.000000 | 0.000000 |
| OVEN | -0.000000 | -0.000000 | 0.000000 | -0.000000 | -0.000000 | -0.000000 | -0.000000 | 0.000000 | 0.000000 | 0.000000 |
| REFR | -0.000000 | -0.000000 | -0.000000 | -0.000000 | -0.000000 | -0.000000 | -0.000000 | -0.000000 | -0.000000 | -0.000000 |
| DENS | 0.048246 | 0.049359 | 0.046588 | 0.047767 | 0.051190 | 0.046928 | 0.046455 | 0.047423 | 0.049179 | 0.048865 |
| FAMRM | 0.057822 | 0.057013 | 0.057238 | 0.059208 | 0.058518 | 0.055123 | 0.057817 | 0.058604 | 0.059895 | 0.057424 |
| HALFB | 0.103928 | 0.102791 | 0.105183 | 0.104379 | 0.103671 | 0.106806 | 0.112708 | 0.104332 | 0.104481 | 0.108234 |
| KITCH | -0.016848 | -0.015641 | -0.015128 | -0.014620 | -0.015921 | -0.015672 | -0.016561 | -0.013676 | -0.016945 | -0.017092 |
| LIVING | 0.005198 | 0.002324 | 0.003951 | 0.004839 | 0.006106 | 0.005630 | 0.003494 | 0.003993 | 0.004532 | 0.004339 |
| OTHFN | 0.038355 | 0.036114 | 0.039843 | 0.035012 | 0.038077 | 0.037492 | 0.034321 | 0.037525 | 0.037721 | 0.035186 |
| RECRM | 0.021484 | 0.021937 | 0.019965 | 0.023502 | 0.024159 | 0.020679 | 0.019380 | 0.020446 | 0.022242 | 0.020969 |
| CLIMB | 0.012317 | 0.006384 | 0.011059 | 0.011721 | 0.016332 | 0.016591 | 0.011285 | 0.013526 | 0.013106 | 0.010781 |
| ELEV | 0.076095 | 0.083937 | 0.078783 | 0.079432 | 0.089403 | 0.078455 | 0.084076 | 0.083452 | 0.082064 | 0.078135 |
| DIRAC | -0.003499 | -0.003454 | -0.002993 | -0.004058 | -0.003754 | -0.002351 | -0.001929 | -0.002463 | -0.001677 | -0.001690 |
| PORCH | -0.018848 | -0.015829 | -0.016723 | -0.014969 | -0.013677 | -0.014311 | -0.015005 | -0.015080 | -0.016535 | -0.013887 |
| AIRSYS | -0.049124 | -0.052072 | -0.052840 | -0.053260 | -0.051097 | -0.050265 | -0.053449 | -0.053212 | -0.052109 | -0.051032 |
| WELL | -0.000000 | 0.000000 | -0.000000 | 0.000000 | -0.000000 | -0.000000 | -0.000000 | -0.000000 | -0.000000 | -0.000000 |
| WELDUS | -0.024269 | -0.024428 | -0.025118 | -0.022449 | -0.024388 | -0.023465 | -0.022414 | -0.023391 | -0.023995 | -0.026031 |
| STEAM | 0.002214 | 0.003292 | 0.000000 | 0.000000 | 0.002270 | 0.002277 | 0.000000 | 0.004752 | 0.002812 | 0.000000 |
| OARSYS | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| noise1 | 0.005424 | 0.002849 | 0.006610 | 0.003614 | 0.006709 | 0.003801 | 0.002519 | 0.005297 | 0.002566 | 0.005736 |
| noise2 | 0.000000 | -0.000000 | -0.000000 | -0.000000 | 0.000000 | 0.000000 | -0.000000 | 0.000000 | 0.000000 | -0.000000 |
| noise3 | 0.000000 | -0.000000 | -0.000000 | 0.000000 | 0.000000 | -0.000000 | -0.000000 | -0.000000 | -0.000000 | -0.000000 |
| noise4 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.001688 | 0.000000 | 0.003442 | 0.000000 | 0.000000 |
| noise5 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000172 |
| noise6 | -0.000805 | -0.001709 | -0.002072 | -0.004038 | -0.001111 | -0.003315 | -0.000000 | -0.004309 | -0.002370 | -0.000000 |
| noise7 | -0.000000 | -0.000000 | -0.000000 | -0.000000 | 0.000000 | 0.000000 | -0.000000 | -0.000000 | -0.000000 | 0.000000 |
| noise8 | 0.003441 | 0.009192 | 0.004116 | 0.002452 | 0.006297 | 0.004724 | 0.005267 | 0.003611 | 0.005380 | 0.002053 |
| noise9 | -0.000000 | 0.000000 | -0.000000 | -0.000000 | -0.000258 | -0.000000 | -0.000000 | -0.000000 | -0.000000 | -0.000000 |
| noise10 | -0.000000 | -0.000000 | -0.000000 | -0.000000 | -0.000000 | -0.000000 | -0.000000 | -0.000000 | -0.000021 | -0.000000 |
| noise11 | -0.008055 | -0.004641 | -0.005265 | -0.002612 | -0.007669 | -0.005447 | -0.007216 | -0.006012 | -0.007707 | -0.003743 |
| noise12 | -0.006468 | -0.007073 | -0.003561 | -0.002931 | -0.006589 | -0.003944 | -0.005517 | -0.002839 | -0.007282 | -0.005623 |
| noise13 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000212 | 0.000000 | 0.000000 | 0.000000 | 0.002019 | 0.000000 |
| noise14 | -0.000124 | -0.000000 | 0.000000 | -0.000000 | -0.000000 | -0.000000 | -0.000000 | 0.000000 | -0.000000 | 0.000000 |
| noise15 | 0.002332 | 0.004505 | 0.004589 | 0.002373 | 0.004535 | 0.003080 | 0.001490 | 0.004166 | 0.004509 | 0.002482 |
| noise16 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | -0.000000 | 0.000000 | 0.000000 | 0.000000 |
| noise17 | -0.002321 | -0.001854 | -0.003085 | -0.001049 | -0.004635 | -0.000000 | -0.000465 | -0.001222 | -0.002072 | -0.002135 |
| noise18 | 0.000274 | 0.000000 | 0.000000 | 0.000704 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.001272 | 0.000000 |
| noise19 | 0.000000 | 0.000000 | -0.000000 | -0.000000 | -0.000000 | -0.000000 | 0.000000 | -0.000000 | -0.000000 | 0.000000 |
| noise20 | -0.000904 | -0.002203 | -0.001322 | -0.000250 | -0.000000 | -0.000180 | -0.001053 | -0.001291 | -0.005082 | -0.000000 |
| ranking | -0.002614 | -0.003632 | -0.000309 | -0.001322 | -0.002222 | -0.000030 | -0.001472 | -0.002578 | -0.000000 | -0.000000 |
As we have seen above, any interpretation needs to take into account the joint distribution of covariates. One possible heuristic is to consider data-driven subgroups. For example, we can analyze what differentiates observations whose predictions are high from those whose predictions are low. The following code estimates a flexible Lasso model with splines, ranks the observations into a few subgroups according to their predicted outcomes, and then estimates the average covariate value for each subgroup.
import itertools
# Number of data-driven subgroups.
nobs = X.shape[0]
# Fold indices
nfold = 5
# Define folds indices
list_1 = [*range(0, nfold, 1)]*nobs
sample = np.random.choice(nobs,nobs, replace=False).tolist()
foldid = [list_1[index] for index in sample]
# Create split function(similar to R)
def split(x, f):
count = max(f) + 1
return tuple( list(itertools.compress(x, (el == i for el in f))) for i in range(count) )
# Split observation indices into folds
list_2 = [*range(0, nobs, 1)]
I = split(list_2, foldid)
# Fit a lasso model.
# Passing foldid argument so we know which observations are in each fold.
lasso_coef_rank=[]
lasso_pred = []
for b in range(0,len(I)):
# Split data - index to keep are in mask as booleans
include_idx = set(I[b]) #Here should go I[b] Set is more efficient, but doesn't reorder your elements if that is desireable
mask = np.array([(i in include_idx) for i in range(len(X))])
# Lasso regression, excluding folds selected
lassocv = LassoCV(random_state=0)
lassocv.fit(scale_X[~mask], Y[~mask])
lasso_coef_rank.append(lassocv.coef_)
lasso_pred.append(lassocv.predict(scale_X[mask]))
y_hat = lasso_pred
df_1 = pd.DataFrame()
for i in [0,1,2,3,4]:
df_2 = pd.DataFrame(y_hat[i])
b = pd.cut(df_2[0], bins =[np.percentile(df_2,0),np.percentile(df_2,25),np.percentile(df_2,50),
np.percentile(df_2,75),np.percentile(df_2,100)], labels = [1,2,3,4])
df_1 = pd.concat([df_1, b])
df_1 = df_1.apply(lambda x: pd.factorize(x)[0])
df_1.rename(columns={0:'ranking'}, inplace=True)
df_1 = df_1.reset_index().drop(columns=['index'])
y = X
x = df_1
y = pd.DataFrame(y)
x = pd.DataFrame(x)
# Ranking observations.
y['ranking'] = x
data = y
# Estimate expected covariate per subgroup
data_frame = pd.DataFrame()
for var_name in covariates:
form = var_name + " ~ " + "0" + "+" + "C(ranking)"
df1 = smf.ols(formula=form, data=data).fit(cov_type = 'HC2').summary2().tables[1].iloc[1:5, :2] #iloc to stay with rankings 0,1,2,3
df1.insert(0, 'covariate', var_name)
df1.insert(3, 'ranking', ['G1','G2','G3','G4'])
df1.insert(4, 'scaling',
pd.DataFrame(norm.cdf((df1['Coef.'] - np.mean(df1['Coef.']))/np.std(df1['Coef.']))))
df1.insert(5, 'variation',
np.std(df1['Coef.'])/np.std(data[var_name]))
label = []
for j in range(0,4):
label += [str(round(df1['Coef.'][j],3)) + " ("
+ str(round(df1['Std.Err.'][j],3)) + ")"]
df1.insert(6, 'labels', label)
df1.reset_index().drop(columns=['index'])
index = []
for m in range(0,4):
index += [str(df1['covariate'][m]) + "_" + "ranking" + str(m+1)]
idx = pd.Index(index)
df1 = df1.set_index(idx)
data_frame = data_frame.append(df1)
data_frame;
labels_data = pd.DataFrame()
for i in range(1,5):
df_mask = data_frame['ranking']==f"G{i}"
filtered_df = data_frame[df_mask].reset_index().drop(columns=['index'])
labels_data[f"ranking{i}"] = filtered_df[['labels']]
labels_data = labels_data.set_index(pd.Index(covariates))
labels_data
| ranking1 | ranking2 | ranking3 | ranking4 | |
|---|---|---|---|---|
| LOT | 49713.31 (1473.048) | 46479.968 (1390.394) | 47806.63 (1427.658) | 47612.513 (1393.569) |
| UNITSF | 2415.869 (24.944) | 2434.834 (24.249) | 2397.706 (23.467) | 2471.907 (26.208) |
| BUILT | 1972.286 (0.301) | 1974.925 (0.294) | 1973.672 (0.299) | 1973.017 (0.299) |
| BATHS | 1.918 (0.009) | 1.975 (0.009) | 1.946 (0.009) | 1.928 (0.009) |
| BEDRMS | 3.218 (0.01) | 3.258 (0.01) | 3.251 (0.01) | 3.243 (0.01) |
| ... | ... | ... | ... | ... |
| noise16 | 0.499 (0.003) | 0.502 (0.003) | 0.498 (0.003) | 0.505 (0.003) |
| noise17 | 0.501 (0.003) | 0.498 (0.003) | 0.502 (0.003) | 0.498 (0.003) |
| noise18 | 0.502 (0.003) | 0.499 (0.003) | 0.5 (0.003) | 0.5 (0.003) |
| noise19 | 0.504 (0.003) | 0.502 (0.003) | 0.498 (0.003) | 0.497 (0.003) |
| noise20 | 0.502 (0.003) | 0.496 (0.003) | 0.501 (0.003) | 0.5 (0.003) |
63 rows × 4 columns
The next heatmap visualizes the results. Note how observations ranked higher (i.e., were predicted to have higher prices) have more bedrooms and baths, were built more recently, have fewer cracks, and so on. The next snippet of code displays the average covariate per group along with each standard errors. The rows are ordered according to \(Var(E[X_{ij} | G_i) / Var(X_i)\), where \(G_i\) denotes the ranking. This is a rough normalized measure of how much variation is “explained” by group membership \(G_i\). Brighter colors indicate larger values.
new_data = pd.DataFrame()
for i in range(0,4):
df_mask = data_frame['ranking']==f"G{i+1}"
filtered_df = data_frame[df_mask]
new_data.insert(i,f"G{i+1}",filtered_df[['scaling']])
new_data;
# plot heatmap
features = covariates
ranks = ['G1','G2','G3','G4']
harvest = np.array(round(new_data,3))
labels_hm = np.array(round(labels_data))
fig, ax = plt.subplots(figsize=(10,15))
# getting the original colormap using cm.get_cmap() function
orig_map = plt.cm.get_cmap('copper')
# reversing the original colormap using reversed() function
reversed_map = orig_map.reversed()
im = ax.imshow(harvest, cmap=reversed_map, aspect='auto')
# make bar
bar = plt.colorbar(im, shrink=0.2)
# show plot with labels
bar.set_label('scaling')
# Setting the labels
ax.set_xticks(np.arange(len(ranks)))
ax.set_yticks(np.arange(len(features)))
# labeling respective list entries
ax.set_xticklabels(ranks)
ax.set_yticklabels(features)
# Rotate the tick labels and set their alignment.
plt.setp(ax.get_xticklabels(), ha="right",
rotation_mode="anchor")
# Creating text annotations by using for loop
for i in range(len(features)):
for j in range(len(ranks)):
text = ax.text(j, i, labels_hm[i, j],
ha="center", va="center", color="w")
ax.set_title("Average covariate values within group (based on prediction ranking)")
fig.tight_layout()
plt.show()

As we just saw above, houses that have, e.g., been built more recently (BUILT), have more baths (BATHS) are associated with larger price predictions.
This sort of interpretation exercise did not rely on reading any coefficients, and in fact it could also be done using any other flexible method, including decisions trees and forests.
2.2.2. Decision Tree¶
This next class of algorithms divides the covariate space into “regions” and estimates a constant prediction within each region.
To estimate a decision tree, we following a recursive partition algorithm. At each stage, we select one variable \(j\) and one split point \(s\), and divide the observations into “left” and “right” subsets, depending on whether \(X_{ij} \leq s\) or \(X_{ij} > s\). For regression problems, the variable and split points are often selected so that the sum of the variances of the outcome variable in each “child” subset is smallest. For classification problems, we split to separate the classes. Then, for each child, we separately repeat the process of finding variables and split points. This continues until a minimum subset size is reached, or improvement falls below some threshold.
At prediction time, to find the predictions for some point \(x\), we just follow the tree we just built, going left or right according to the selected variables and split points, until we reach a terminal node. Then, for regression problems, the predicted value at some point \(x\) is the average outcome of the observations in the same partition as the point \(x\). For classification problems, we output the majority class in the node.
from sklearn.tree import DecisionTreeRegressor
import graphviz
from sklearn import tree
from sklearn.tree import export_graphviz
from sklearn.metrics import accuracy_score
from pandas import Series
from simple_colors import *
import statsmodels.api as sm
import statsmodels.formula.api as smf
from scipy.stats import norm
from sklearn.metrics import accuracy_score
from sklearn import metrics
from sklearn.metrics import r2_score
import matplotlib.pyplot as plt
from sklearn import tree
from sklearn.model_selection import train_test_split
# Fit tree without pruning first
XX = data.loc[:,covariates]
dt = DecisionTreeRegressor(ccp_alpha=0, max_depth= 15, random_state=0)
x_train, x_test, y_train, y_test = train_test_split(XX.to_numpy(), Y, test_size=.3)
tree1 = dt.fit(x_train,y_train)
At this point, we have not constrained the complexity of the tree in any way, so it’s likely too deep and probably overfits. Here’s a plot of what we have so far (without bothering to label the splits to avoid clutter).
from sklearn import tree
plt.figure(figsize=(18,5))
tree.plot_tree(dt)
[Text(0.6649812429236953, 0.96875, 'X[22] <= 3.5\nsquared_error = 0.953\nsamples = 20108\nvalue = 11.817'),
Text(0.41149011719399203, 0.90625, 'X[1] <= 2436.5\nsquared_error = 0.765\nsamples = 19394\nvalue = 11.888'),
Text(0.1962294981926209, 0.84375, 'X[3] <= 1.5\nsquared_error = 0.641\nsamples = 13894\nvalue = 11.685'),
Text(0.08274342487950806, 0.78125, 'X[19] <= 1.5\nsquared_error = 0.692\nsamples = 5053\nvalue = 11.39'),
Text(0.032513347598471, 0.71875, 'X[54] <= 0.001\nsquared_error = 0.585\nsamples = 2640\nvalue = 11.546'),
Text(0.032180956041216555, 0.65625, 'squared_error = 0.0\nsamples = 1\nvalue = 0.0'),
Text(0.032845739155725445, 0.65625, 'X[34] <= 2.154\nsquared_error = 0.534\nsamples = 2639\nvalue = 11.55'),
Text(0.004731386072793751, 0.59375, 'X[53] <= 0.008\nsquared_error = 1.991\nsamples = 164\nvalue = 11.158'),
Text(0.0006647831145088915, 0.53125, 'X[38] <= 1.5\nsquared_error = 35.102\nsamples = 2\nvalue = 5.925'),
Text(0.00033239155725444574, 0.46875, 'squared_error = 0.0\nsamples = 1\nvalue = 0.0'),
Text(0.0009971746717633372, 0.46875, 'squared_error = 0.0\nsamples = 1\nvalue = 11.849'),
Text(0.008797989031078611, 0.53125, 'X[49] <= 0.109\nsquared_error = 1.24\nsamples = 162\nvalue = 11.223'),
Text(0.0016619577862722287, 0.46875, 'X[58] <= 0.159\nsquared_error = 7.439\nsamples = 16\nvalue = 9.978'),
Text(0.001329566229017783, 0.40625, 'squared_error = 0.0\nsamples = 1\nvalue = 0.0'),
Text(0.0019943493435266744, 0.40625, 'X[57] <= 0.284\nsquared_error = 0.856\nsamples = 15\nvalue = 10.643'),
Text(0.0006647831145088915, 0.34375, 'X[9] <= 1.5\nsquared_error = 0.159\nsamples = 2\nvalue = 8.811'),
Text(0.00033239155725444574, 0.28125, 'squared_error = 0.0\nsamples = 1\nvalue = 9.21'),
Text(0.0009971746717633372, 0.28125, 'squared_error = -0.0\nsamples = 1\nvalue = 8.412'),
Text(0.0033239155725444574, 0.34375, 'X[52] <= 0.229\nsquared_error = 0.367\nsamples = 13\nvalue = 10.925'),
Text(0.0016619577862722287, 0.28125, 'X[62] <= 0.531\nsquared_error = 0.116\nsamples = 4\nvalue = 10.244'),
Text(0.001329566229017783, 0.21875, 'squared_error = 0.0\nsamples = 2\nvalue = 9.903'),
Text(0.0019943493435266744, 0.21875, 'X[52] <= 0.109\nsquared_error = 0.0\nsamples = 2\nvalue = 10.584'),
Text(0.0016619577862722287, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 10.597'),
Text(0.00232674090078112, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 10.571'),
Text(0.0049858733588166865, 0.28125, 'X[58] <= 0.621\nsquared_error = 0.181\nsamples = 9\nvalue = 11.227'),
Text(0.003656307129798903, 0.21875, 'X[5] <= 0.5\nsquared_error = 0.045\nsamples = 5\nvalue = 11.499'),
Text(0.0029915240152900116, 0.15625, 'X[2] <= 1987.5\nsquared_error = 0.009\nsamples = 3\nvalue = 11.648'),
Text(0.002659132458035566, 0.09375, 'X[29] <= 0.5\nsquared_error = 0.0\nsamples = 2\nvalue = 11.716'),
Text(0.00232674090078112, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.695'),
Text(0.0029915240152900116, 0.03125, 'squared_error = -0.0\nsamples = 1\nvalue = 11.736'),
Text(0.0033239155725444574, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.513'),
Text(0.004321090244307795, 0.15625, 'X[49] <= 0.044\nsquared_error = 0.014\nsamples = 2\nvalue = 11.276'),
Text(0.003988698687053349, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.396'),
Text(0.00465348180156224, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 11.156'),
Text(0.006315439587834469, 0.21875, 'X[55] <= 0.655\nsquared_error = 0.143\nsamples = 4\nvalue = 10.887'),
Text(0.005650656473325578, 0.15625, 'X[51] <= 0.511\nsquared_error = 0.004\nsamples = 2\nvalue = 10.53'),
Text(0.005318264916071132, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 10.463'),
Text(0.005983048030580023, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 10.597'),
Text(0.006980222702343361, 0.15625, 'X[60] <= 0.468\nsquared_error = 0.026\nsamples = 2\nvalue = 11.245'),
Text(0.006647831145088915, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.082'),
Text(0.007312614259597806, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.408'),
Text(0.015934020275884992, 0.46875, 'X[49] <= 0.506\nsquared_error = 0.372\nsamples = 146\nvalue = 11.359'),
Text(0.011592155559248795, 0.40625, 'X[62] <= 0.297\nsquared_error = 0.457\nsamples = 54\nvalue = 11.149'),
Text(0.008891474156556424, 0.34375, 'X[46] <= 0.257\nsquared_error = 0.181\nsamples = 10\nvalue = 11.81'),
Text(0.007977397374106698, 0.28125, 'X[34] <= 1.5\nsquared_error = 0.042\nsamples = 2\nvalue = 11.174'),
Text(0.007645005816852252, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 10.968'),
Text(0.008309788931361143, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 11.379'),
Text(0.009805550939006149, 0.28125, 'X[1] <= 1525.0\nsquared_error = 0.09\nsamples = 8\nvalue = 11.97'),
Text(0.008974572045870035, 0.21875, 'X[45] <= 0.765\nsquared_error = 0.036\nsamples = 6\nvalue = 12.11'),
Text(0.008309788931361143, 0.15625, 'X[1] <= 1175.0\nsquared_error = 0.013\nsamples = 3\nvalue = 12.28'),
Text(0.007977397374106698, 0.09375, 'X[54] <= 0.243\nsquared_error = 0.003\nsamples = 2\nvalue = 12.205'),
Text(0.007645005816852252, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 12.255'),
Text(0.008309788931361143, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 12.155'),
Text(0.00864218048861559, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 12.429'),
Text(0.009639355160378926, 0.15625, 'X[54] <= 0.637\nsquared_error = 0.002\nsamples = 3\nvalue = 11.94'),
Text(0.00930696360312448, 0.09375, 'X[4] <= 1.5\nsquared_error = 0.0\nsamples = 2\nvalue = 11.967'),
Text(0.008974572045870035, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.983'),
Text(0.009639355160378926, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.951'),
Text(0.009971746717633373, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.884'),
Text(0.010636529832142264, 0.21875, 'X[60] <= 0.523\nsquared_error = 0.014\nsamples = 2\nvalue = 11.55'),
Text(0.010304138274887818, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 11.43'),
Text(0.010968921389396709, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 11.67'),
Text(0.014292836961941167, 0.34375, 'X[43] <= 0.031\nsquared_error = 0.398\nsamples = 44\nvalue = 10.999'),
Text(0.013960445404686722, 0.28125, 'squared_error = 0.0\nsamples = 1\nvalue = 8.923'),
Text(0.014625228519195612, 0.28125, 'X[2] <= 1987.5\nsquared_error = 0.305\nsamples = 43\nvalue = 11.048'),
Text(0.012963270732923384, 0.21875, 'X[53] <= 0.538\nsquared_error = 0.266\nsamples = 39\nvalue = 10.97'),
Text(0.011633704503905601, 0.15625, 'X[52] <= 0.264\nsquared_error = 0.196\nsamples = 19\nvalue = 10.728'),
Text(0.010968921389396709, 0.09375, 'X[54] <= 0.598\nsquared_error = 0.081\nsamples = 5\nvalue = 11.179'),
Text(0.010636529832142264, 0.03125, 'squared_error = 0.034\nsamples = 4\nvalue = 11.295'),
Text(0.011301312946651156, 0.03125, 'squared_error = -0.0\nsamples = 1\nvalue = 10.714'),
Text(0.012298487618414492, 0.09375, 'X[46] <= 0.946\nsquared_error = 0.138\nsamples = 14\nvalue = 10.567'),
Text(0.011966096061160046, 0.03125, 'squared_error = 0.083\nsamples = 11\nvalue = 10.427'),
Text(0.012630879175668939, 0.03125, 'squared_error = 0.004\nsamples = 3\nvalue = 11.08'),
Text(0.014292836961941167, 0.15625, 'X[58] <= 0.343\nsquared_error = 0.224\nsamples = 20\nvalue = 11.2'),
Text(0.013628053847432275, 0.09375, 'X[54] <= 0.983\nsquared_error = 0.063\nsamples = 5\nvalue = 11.752'),
Text(0.01329566229017783, 0.03125, 'squared_error = 0.012\nsamples = 4\nvalue = 11.868'),
Text(0.013960445404686722, 0.03125, 'squared_error = -0.0\nsamples = 1\nvalue = 11.29'),
Text(0.014957620076450058, 0.09375, 'X[41] <= 0.5\nsquared_error = 0.142\nsamples = 15\nvalue = 11.016'),
Text(0.014625228519195612, 0.03125, 'squared_error = 0.082\nsamples = 12\nvalue = 10.883'),
Text(0.015290011633704505, 0.03125, 'squared_error = 0.031\nsamples = 3\nvalue = 11.546'),
Text(0.01628718630546784, 0.21875, 'X[47] <= 0.564\nsquared_error = 0.05\nsamples = 4\nvalue = 11.805'),
Text(0.015954794748213395, 0.15625, 'X[62] <= 0.659\nsquared_error = 0.013\nsamples = 3\nvalue = 11.689'),
Text(0.01562240319095895, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.849'),
Text(0.01628718630546784, 0.09375, 'squared_error = -0.0\nsamples = 2\nvalue = 11.608'),
Text(0.016619577862722286, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 12.155'),
Text(0.02027588499252119, 0.40625, 'X[56] <= 0.087\nsquared_error = 0.281\nsamples = 92\nvalue = 11.483'),
Text(0.01794914409174007, 0.34375, 'X[54] <= 0.387\nsquared_error = 0.184\nsamples = 6\nvalue = 12.157'),
Text(0.01728436097723118, 0.28125, 'X[34] <= 0.5\nsquared_error = 0.025\nsamples = 3\nvalue = 12.541'),
Text(0.01695196941997673, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 12.766'),
Text(0.017616752534485625, 0.21875, 'squared_error = 0.0\nsamples = 2\nvalue = 12.429'),
Text(0.01861392720624896, 0.28125, 'X[48] <= 0.793\nsquared_error = 0.047\nsamples = 3\nvalue = 11.772'),
Text(0.018281535648994516, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 12.044'),
Text(0.018946318763503407, 0.21875, 'X[60] <= 0.592\nsquared_error = 0.015\nsamples = 2\nvalue = 11.636'),
Text(0.01861392720624896, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 11.513'),
Text(0.019278710320757852, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 11.76'),
Text(0.022602625893302312, 0.34375, 'X[46] <= 0.014\nsquared_error = 0.254\nsamples = 86\nvalue = 11.436'),
Text(0.022270234336047863, 0.28125, 'squared_error = 0.0\nsamples = 1\nvalue = 9.999'),
Text(0.022935017450556757, 0.28125, 'X[47] <= 0.941\nsquared_error = 0.232\nsamples = 85\nvalue = 11.453'),
Text(0.021273059664284527, 0.21875, 'X[46] <= 0.054\nsquared_error = 0.212\nsamples = 82\nvalue = 11.481'),
Text(0.019943493435266746, 0.15625, 'X[54] <= 0.707\nsquared_error = 0.146\nsamples = 4\nvalue = 12.15'),
Text(0.019278710320757852, 0.09375, 'X[57] <= 0.608\nsquared_error = 0.035\nsamples = 2\nvalue = 11.796'),
Text(0.018946318763503407, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.608'),
Text(0.019611101878012297, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.983'),
Text(0.020608276549775636, 0.09375, 'X[50] <= 0.304\nsquared_error = 0.006\nsamples = 2\nvalue = 12.503'),
Text(0.02027588499252119, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 12.429'),
Text(0.020940668107030082, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 12.578'),
Text(0.022602625893302312, 0.15625, 'X[29] <= 1.5\nsquared_error = 0.191\nsamples = 78\nvalue = 11.447'),
Text(0.021937842778793418, 0.09375, 'X[58] <= 0.048\nsquared_error = 0.171\nsamples = 74\nvalue = 11.414'),
Text(0.021605451221538972, 0.03125, 'squared_error = 0.011\nsamples = 2\nvalue = 10.493'),
Text(0.022270234336047863, 0.03125, 'squared_error = 0.151\nsamples = 72\nvalue = 11.439'),
Text(0.023267409007811202, 0.09375, 'X[58] <= 0.357\nsquared_error = 0.157\nsamples = 4\nvalue = 12.065'),
Text(0.022935017450556757, 0.03125, 'squared_error = 0.001\nsamples = 2\nvalue = 12.458'),
Text(0.023599800565065648, 0.03125, 'squared_error = 0.004\nsamples = 2\nvalue = 11.672'),
Text(0.024596975236828984, 0.21875, 'X[7] <= 1.5\nsquared_error = 0.16\nsamples = 3\nvalue = 10.666'),
Text(0.02426458367957454, 0.15625, 'X[47] <= 0.948\nsquared_error = 0.006\nsamples = 2\nvalue = 10.386'),
Text(0.023932192122320093, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 10.309'),
Text(0.024596975236828984, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 10.463'),
Text(0.02492936679408343, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 11.225'),
Text(0.060960092238657136, 0.59375, 'X[8] <= 3.5\nsquared_error = 0.427\nsamples = 2475\nvalue = 11.576'),
Text(0.04463914741565564, 0.53125, 'X[28] <= 0.5\nsquared_error = 0.414\nsamples = 2258\nvalue = 11.548'),
Text(0.031556423466843946, 0.46875, 'X[46] <= 0.008\nsquared_error = 0.452\nsamples = 1871\nvalue = 11.51'),
Text(0.0254279541299651, 0.40625, 'X[50] <= 0.205\nsquared_error = 9.283\nsamples = 7\nvalue = 9.735'),
Text(0.024596975236828984, 0.34375, 'X[61] <= 0.388\nsquared_error = 0.022\nsamples = 2\nvalue = 4.927'),
Text(0.02426458367957454, 0.28125, 'squared_error = 0.0\nsamples = 1\nvalue = 4.779'),
Text(0.02492936679408343, 0.28125, 'squared_error = 0.0\nsamples = 1\nvalue = 5.075'),
Text(0.026258933023101214, 0.34375, 'X[60] <= 0.731\nsquared_error = 0.041\nsamples = 5\nvalue = 11.659'),
Text(0.025594149908592323, 0.28125, 'X[49] <= 0.499\nsquared_error = 0.007\nsamples = 2\nvalue = 11.432'),
Text(0.025261758351337878, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 11.35'),
Text(0.02592654146584677, 0.21875, 'squared_error = -0.0\nsamples = 1\nvalue = 11.513'),
Text(0.026923716137610104, 0.28125, 'X[8] <= 2.5\nsquared_error = 0.006\nsamples = 3\nvalue = 11.81'),
Text(0.02659132458035566, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 11.918'),
Text(0.02725610769486455, 0.21875, 'X[44] <= 0.704\nsquared_error = 0.0\nsamples = 2\nvalue = 11.756'),
Text(0.026923716137610104, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 11.775'),
Text(0.027588499252118995, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 11.736'),
Text(0.03768489280372279, 0.40625, 'X[1] <= 2415.0\nsquared_error = 0.407\nsamples = 1864\nvalue = 11.516'),
Text(0.03357154728269902, 0.34375, 'X[1] <= 1277.0\nsquared_error = 0.404\nsamples = 1608\nvalue = 11.55'),
Text(0.03066312115672262, 0.28125, 'X[58] <= 0.956\nsquared_error = 0.315\nsamples = 709\nvalue = 11.446'),
Text(0.029084261259764002, 0.21875, 'X[1] <= 1073.0\nsquared_error = 0.262\nsamples = 668\nvalue = 11.467'),
Text(0.02825328236662789, 0.15625, 'X[55] <= 0.019\nsquared_error = 0.314\nsamples = 308\nvalue = 11.376'),
Text(0.027588499252118995, 0.09375, 'X[2] <= 1972.5\nsquared_error = 3.618\nsamples = 11\nvalue = 10.657'),
Text(0.02725610769486455, 0.03125, 'squared_error = 0.293\nsamples = 10\nvalue = 11.236'),
Text(0.027920890809373444, 0.03125, 'squared_error = -0.0\nsamples = 1\nvalue = 4.868'),
Text(0.02891806548113678, 0.09375, 'X[42] <= -2.5\nsquared_error = 0.171\nsamples = 297\nvalue = 11.403'),
Text(0.028585673923882334, 0.03125, 'squared_error = 0.166\nsamples = 50\nvalue = 11.159'),
Text(0.029250457038391225, 0.03125, 'squared_error = 0.158\nsamples = 247\nvalue = 11.452'),
Text(0.029915240152900115, 0.15625, 'X[47] <= 0.006\nsquared_error = 0.205\nsamples = 360\nvalue = 11.544'),
Text(0.02958284859564567, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 8.517'),
Text(0.03024763171015456, 0.09375, 'X[45] <= 0.015\nsquared_error = 0.18\nsamples = 359\nvalue = 11.553'),
Text(0.029915240152900115, 0.03125, 'squared_error = 0.181\nsamples = 3\nvalue = 12.551'),
Text(0.03058002326740901, 0.03125, 'squared_error = 0.171\nsamples = 356\nvalue = 11.544'),
Text(0.032241981053681236, 0.21875, 'X[57] <= 0.927\nsquared_error = 1.054\nsamples = 41\nvalue = 11.102'),
Text(0.03190958949642679, 0.15625, 'X[54] <= 0.964\nsquared_error = 0.149\nsamples = 40\nvalue = 11.253'),
Text(0.031577197939172345, 0.09375, 'X[6] <= 1.5\nsquared_error = 0.109\nsamples = 39\nvalue = 11.286'),
Text(0.0312448063819179, 0.03125, 'squared_error = 0.099\nsamples = 10\nvalue = 10.998'),
Text(0.03190958949642679, 0.03125, 'squared_error = 0.073\nsamples = 29\nvalue = 11.386'),
Text(0.032241981053681236, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 9.952'),
Text(0.03257437261093568, 0.15625, 'squared_error = -0.0\nsamples = 1\nvalue = 5.075'),
Text(0.03647997340867542, 0.28125, 'X[45] <= 0.989\nsquared_error = 0.459\nsamples = 899\nvalue = 11.632'),
Text(0.034402526175835134, 0.21875, 'X[44] <= 0.043\nsquared_error = 0.349\nsamples = 892\nvalue = 11.644'),
Text(0.03323915572544457, 0.15625, 'X[56] <= 0.037\nsquared_error = 2.439\nsamples = 37\nvalue = 11.191'),
Text(0.03290676416819013, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 4.754'),
Text(0.03357154728269902, 0.09375, 'X[58] <= 0.037\nsquared_error = 1.323\nsamples = 36\nvalue = 11.37'),
Text(0.03323915572544457, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 5.298'),
Text(0.03390393883995346, 0.03125, 'squared_error = 0.278\nsamples = 35\nvalue = 11.543'),
Text(0.035565896626225696, 0.15625, 'X[29] <= 1.5\nsquared_error = 0.249\nsamples = 855\nvalue = 11.663'),
Text(0.034901113511716805, 0.09375, 'X[46] <= 0.999\nsquared_error = 0.236\nsamples = 825\nvalue = 11.646'),
Text(0.03456872195446236, 0.03125, 'squared_error = 0.229\nsamples = 824\nvalue = 11.649'),
Text(0.03523350506897125, 0.03125, 'squared_error = -0.0\nsamples = 1\nvalue = 9.21'),
Text(0.036230679740734587, 0.09375, 'X[33] <= 0.5\nsquared_error = 0.37\nsamples = 30\nvalue = 12.144'),
Text(0.03589828818348014, 0.03125, 'squared_error = 0.23\nsamples = 28\nvalue = 12.041'),
Text(0.03656307129798903, 0.03125, 'squared_error = 0.08\nsamples = 2\nvalue = 13.588'),
Text(0.038557420641515704, 0.21875, 'X[50] <= 0.875\nsquared_error = 12.499\nsamples = 7\nvalue = 10.199'),
Text(0.03822502908426126, 0.15625, 'X[46] <= 0.747\nsquared_error = 0.235\nsamples = 6\nvalue = 11.631'),
Text(0.03756024596975237, 0.09375, 'X[46] <= 0.588\nsquared_error = 0.067\nsamples = 3\nvalue = 12.052'),
Text(0.03722785441249792, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.704'),
Text(0.03789263752700681, 0.03125, 'squared_error = 0.01\nsamples = 2\nvalue = 12.226'),
Text(0.03888981219877015, 0.09375, 'X[60] <= 0.319\nsquared_error = 0.049\nsamples = 3\nvalue = 11.21'),
Text(0.038557420641515704, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 10.915'),
Text(0.039222203756024594, 0.03125, 'squared_error = 0.009\nsamples = 2\nvalue = 11.358'),
Text(0.03888981219877015, 0.15625, 'squared_error = -0.0\nsamples = 1\nvalue = 1.609'),
Text(0.04179823832474655, 0.34375, 'X[44] <= 0.096\nsquared_error = 0.373\nsamples = 256\nvalue = 11.305'),
Text(0.04055176998504238, 0.28125, 'X[49] <= 0.857\nsquared_error = 0.819\nsamples = 22\nvalue = 10.857'),
Text(0.04021937842778794, 0.21875, 'X[45] <= 0.053\nsquared_error = 0.585\nsamples = 21\nvalue = 10.969'),
Text(0.03988698687053349, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 8.923'),
Text(0.04055176998504238, 0.15625, 'X[53] <= 0.897\nsquared_error = 0.395\nsamples = 20\nvalue = 11.071'),
Text(0.04021937842778794, 0.09375, 'X[49] <= 0.119\nsquared_error = 0.243\nsamples = 19\nvalue = 11.164'),
Text(0.03988698687053349, 0.03125, 'squared_error = 0.066\nsamples = 4\nvalue = 10.55'),
Text(0.04055176998504238, 0.03125, 'squared_error = 0.163\nsamples = 15\nvalue = 11.328'),
Text(0.04088416154229683, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 9.306'),
Text(0.04088416154229683, 0.21875, 'squared_error = -0.0\nsamples = 1\nvalue = 8.517'),
Text(0.043044706664450726, 0.28125, 'X[56] <= 0.003\nsquared_error = 0.31\nsamples = 234\nvalue = 11.347'),
Text(0.04271231510719628, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 9.21'),
Text(0.04337709822170517, 0.21875, 'X[0] <= 94000.0\nsquared_error = 0.292\nsamples = 233\nvalue = 11.356'),
Text(0.04221372777131461, 0.15625, 'X[59] <= 0.535\nsquared_error = 0.278\nsamples = 218\nvalue = 11.323'),
Text(0.04154894465680572, 0.09375, 'X[50] <= 0.745\nsquared_error = 0.232\nsamples = 114\nvalue = 11.425'),
Text(0.04121655309955127, 0.03125, 'squared_error = 0.194\nsamples = 87\nvalue = 11.518'),
Text(0.041881336214060164, 0.03125, 'squared_error = 0.237\nsamples = 27\nvalue = 11.126'),
Text(0.0428785108858235, 0.09375, 'X[55] <= 0.989\nsquared_error = 0.304\nsamples = 104\nvalue = 11.211'),
Text(0.042546119328569054, 0.03125, 'squared_error = 0.282\nsamples = 103\nvalue = 11.226'),
Text(0.043210902443077945, 0.03125, 'squared_error = -0.0\nsamples = 1\nvalue = 9.616'),
Text(0.044540468672095726, 0.15625, 'X[48] <= 0.939\nsquared_error = 0.246\nsamples = 15\nvalue = 11.834'),
Text(0.04420807711484128, 0.09375, 'X[57] <= 0.38\nsquared_error = 0.137\nsamples = 14\nvalue = 11.742'),
Text(0.043875685557586835, 0.03125, 'squared_error = 0.028\nsamples = 2\nvalue = 10.988'),
Text(0.044540468672095726, 0.03125, 'squared_error = 0.044\nsamples = 12\nvalue = 11.868'),
Text(0.04487286022935017, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 13.122'),
Text(0.05772187136446734, 0.46875, 'X[1] <= 1504.5\nsquared_error = 0.185\nsamples = 387\nvalue = 11.735'),
Text(0.05287103207578527, 0.40625, 'X[50] <= 0.989\nsquared_error = 0.209\nsamples = 135\nvalue = 11.623'),
Text(0.050897457204587, 0.34375, 'X[56] <= 0.129\nsquared_error = 0.173\nsamples = 132\nvalue = 11.602'),
Text(0.0486953631377763, 0.28125, 'X[58] <= 0.958\nsquared_error = 0.44\nsamples = 19\nvalue = 11.289'),
Text(0.04753199268738574, 0.21875, 'X[61] <= 0.555\nsquared_error = 0.116\nsamples = 17\nvalue = 11.488'),
Text(0.04620242645836796, 0.15625, 'X[0] <= 40284.602\nsquared_error = 0.03\nsamples = 9\nvalue = 11.285'),
Text(0.04553764334385907, 0.09375, 'X[43] <= 0.386\nsquared_error = 0.012\nsamples = 7\nvalue = 11.356'),
Text(0.045205251786604624, 0.03125, 'squared_error = 0.002\nsamples = 3\nvalue = 11.457'),
Text(0.045870034901113514, 0.03125, 'squared_error = 0.006\nsamples = 4\nvalue = 11.281'),
Text(0.04686720957287685, 0.09375, 'X[61] <= 0.464\nsquared_error = 0.015\nsamples = 2\nvalue = 11.036'),
Text(0.046534818015622405, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.156'),
Text(0.047199601130131295, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 10.915'),
Text(0.04886155891640352, 0.15625, 'X[48] <= 0.221\nsquared_error = 0.115\nsamples = 8\nvalue = 11.716'),
Text(0.04819677580189463, 0.09375, 'X[45] <= 0.294\nsquared_error = 0.005\nsamples = 2\nvalue = 11.222'),
Text(0.047864384244640186, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.29'),
Text(0.04852916735914908, 0.03125, 'squared_error = -0.0\nsamples = 1\nvalue = 11.155'),
Text(0.04952634203091241, 0.09375, 'X[6] <= 4.5\nsquared_error = 0.043\nsamples = 6\nvalue = 11.881'),
Text(0.04919395047365797, 0.03125, 'squared_error = 0.01\nsamples = 3\nvalue = 12.049'),
Text(0.04985873358816686, 0.03125, 'squared_error = 0.021\nsamples = 3\nvalue = 11.713'),
Text(0.04985873358816686, 0.21875, 'X[41] <= 0.5\nsquared_error = 0.0\nsamples = 2\nvalue = 9.599'),
Text(0.04952634203091241, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 9.616'),
Text(0.0501911251454213, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 9.582'),
Text(0.053099551271397705, 0.28125, 'X[27] <= 0.5\nsquared_error = 0.109\nsamples = 113\nvalue = 11.654'),
Text(0.052019278710320756, 0.21875, 'X[0] <= 302841.5\nsquared_error = 0.089\nsamples = 110\nvalue = 11.636'),
Text(0.051188299817184646, 0.15625, 'X[36] <= 1.761\nsquared_error = 0.077\nsamples = 106\nvalue = 11.652'),
Text(0.0508559082599302, 0.09375, 'X[51] <= 0.961\nsquared_error = 0.071\nsamples = 105\nvalue = 11.66'),
Text(0.050523516702675755, 0.03125, 'squared_error = 0.067\nsamples = 102\nvalue = 11.647'),
Text(0.051188299817184646, 0.03125, 'squared_error = 0.016\nsamples = 3\nvalue = 12.093'),
Text(0.05152069137443909, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 10.82'),
Text(0.05285025760345687, 0.15625, 'X[50] <= 0.538\nsquared_error = 0.225\nsamples = 4\nvalue = 11.204'),
Text(0.05218547448894798, 0.09375, 'X[57] <= 0.427\nsquared_error = 0.023\nsamples = 2\nvalue = 11.663'),
Text(0.05185308293169354, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.813'),
Text(0.05251786604620243, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.513'),
Text(0.05351504071796576, 0.09375, 'X[48] <= 0.165\nsquared_error = 0.006\nsamples = 2\nvalue = 10.744'),
Text(0.05318264916071132, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 10.669'),
Text(0.05384743227522021, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 10.82'),
Text(0.054179823832474654, 0.21875, 'X[57] <= 0.149\nsquared_error = 0.367\nsamples = 3\nvalue = 12.327'),
Text(0.05384743227522021, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 13.122'),
Text(0.0545122153897291, 0.15625, 'X[9] <= 1.5\nsquared_error = 0.077\nsamples = 2\nvalue = 11.929'),
Text(0.054179823832474654, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 12.206'),
Text(0.054844606946983544, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 11.653'),
Text(0.054844606946983544, 0.34375, 'X[61] <= 0.303\nsquared_error = 0.837\nsamples = 3\nvalue = 12.58'),
Text(0.0545122153897291, 0.28125, 'squared_error = 0.0\nsamples = 1\nvalue = 13.872'),
Text(0.05517699850423799, 0.28125, 'X[54] <= 0.414\nsquared_error = 0.002\nsamples = 2\nvalue = 11.934'),
Text(0.054844606946983544, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 11.983'),
Text(0.055509390061492435, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 11.884'),
Text(0.06257271065314941, 0.40625, 'X[0] <= 10900.0\nsquared_error = 0.161\nsamples = 252\nvalue = 11.795'),
Text(0.05916569719129134, 0.34375, 'X[51] <= 0.006\nsquared_error = 0.131\nsamples = 92\nvalue = 11.692'),
Text(0.058833305634036895, 0.28125, 'squared_error = 0.0\nsamples = 1\nvalue = 10.309'),
Text(0.059498088748545785, 0.28125, 'X[8] <= 2.5\nsquared_error = 0.111\nsamples = 91\nvalue = 11.707'),
Text(0.05700515206913744, 0.21875, 'X[50] <= 0.042\nsquared_error = 0.086\nsamples = 79\nvalue = 11.66'),
Text(0.05584178161874689, 0.15625, 'X[47] <= 0.283\nsquared_error = 0.046\nsamples = 4\nvalue = 11.163'),
Text(0.055509390061492435, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 10.82'),
Text(0.05617417317600133, 0.09375, 'X[62] <= 0.875\nsquared_error = 0.009\nsamples = 3\nvalue = 11.277'),
Text(0.05584178161874689, 0.03125, 'squared_error = 0.0\nsamples = 2\nvalue = 11.212'),
Text(0.05650656473325578, 0.03125, 'squared_error = -0.0\nsamples = 1\nvalue = 11.408'),
Text(0.058168522519528004, 0.15625, 'X[44] <= 0.911\nsquared_error = 0.074\nsamples = 75\nvalue = 11.687'),
Text(0.057503739405019114, 0.09375, 'X[50] <= 0.987\nsquared_error = 0.069\nsamples = 65\nvalue = 11.723'),
Text(0.05717134784776467, 0.03125, 'squared_error = 0.063\nsamples = 64\nvalue = 11.713'),
Text(0.05783613096227356, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 12.388'),
Text(0.058833305634036895, 0.09375, 'X[50] <= 0.878\nsquared_error = 0.048\nsamples = 10\nvalue = 11.453'),
Text(0.05850091407678245, 0.03125, 'squared_error = 0.006\nsamples = 5\nvalue = 11.289'),
Text(0.05916569719129134, 0.03125, 'squared_error = 0.037\nsamples = 5\nvalue = 11.616'),
Text(0.06199102542795413, 0.21875, 'X[2] <= 1955.0\nsquared_error = 0.17\nsamples = 12\nvalue = 12.011'),
Text(0.06082765497756357, 0.15625, 'X[43] <= 0.94\nsquared_error = 0.033\nsamples = 8\nvalue = 12.27'),
Text(0.060162871863054676, 0.09375, 'X[48] <= 0.219\nsquared_error = 0.007\nsamples = 5\nvalue = 12.146'),
Text(0.05983048030580023, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 12.301'),
Text(0.06049526342030912, 0.03125, 'squared_error = 0.001\nsamples = 4\nvalue = 12.107'),
Text(0.061492438092072464, 0.09375, 'X[1] <= 2125.5\nsquared_error = 0.009\nsamples = 3\nvalue = 12.476'),
Text(0.06116004653481802, 0.03125, 'squared_error = 0.0\nsamples = 2\nvalue = 12.409'),
Text(0.06182482964932691, 0.03125, 'squared_error = -0.0\nsamples = 1\nvalue = 12.612'),
Text(0.06315439587834469, 0.15625, 'X[53] <= 0.984\nsquared_error = 0.042\nsamples = 4\nvalue = 11.493'),
Text(0.06282200432109024, 0.09375, 'X[6] <= 4.0\nsquared_error = 0.006\nsamples = 3\nvalue = 11.605'),
Text(0.0624896127638358, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.513'),
Text(0.06315439587834469, 0.03125, 'squared_error = 0.002\nsamples = 2\nvalue = 11.652'),
Text(0.06348678743559913, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 11.156'),
Text(0.06597972411500748, 0.34375, 'X[45] <= 0.005\nsquared_error = 0.169\nsamples = 160\nvalue = 11.854'),
Text(0.06564733255775303, 0.28125, 'squared_error = 0.0\nsamples = 1\nvalue = 10.597'),
Text(0.06631211567226192, 0.28125, 'X[47] <= 0.988\nsquared_error = 0.16\nsamples = 159\nvalue = 11.862'),
Text(0.06597972411500748, 0.21875, 'X[2] <= 1935.0\nsquared_error = 0.151\nsamples = 158\nvalue = 11.87'),
Text(0.06481635366461692, 0.15625, 'X[1] <= 2250.0\nsquared_error = 0.326\nsamples = 12\nvalue = 12.171'),
Text(0.06415157055010803, 0.09375, 'X[44] <= 0.152\nsquared_error = 0.155\nsamples = 8\nvalue = 11.869'),
Text(0.06381917899285358, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.002'),
Text(0.06448396210736247, 0.03125, 'squared_error = 0.054\nsamples = 7\nvalue = 11.993'),
Text(0.06548113677912581, 0.09375, 'X[46] <= 0.72\nsquared_error = 0.121\nsamples = 4\nvalue = 12.776'),
Text(0.06514874522187136, 0.03125, 'squared_error = 0.015\nsamples = 2\nvalue = 13.095'),
Text(0.06581352833638025, 0.03125, 'squared_error = 0.024\nsamples = 2\nvalue = 12.456'),
Text(0.06714309456539803, 0.15625, 'X[0] <= 545401.0\nsquared_error = 0.129\nsamples = 146\nvalue = 11.845'),
Text(0.0668107030081436, 0.09375, 'X[56] <= 0.156\nsquared_error = 0.122\nsamples = 145\nvalue = 11.853'),
Text(0.06647831145088914, 0.03125, 'squared_error = 0.124\nsamples = 29\nvalue = 11.69'),
Text(0.06714309456539803, 0.03125, 'squared_error = 0.114\nsamples = 116\nvalue = 11.893'),
Text(0.06747548612265249, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 10.82'),
Text(0.06664450722951637, 0.21875, 'squared_error = -0.0\nsamples = 1\nvalue = 10.597'),
Text(0.07728103706165863, 0.53125, 'X[53] <= 0.022\nsquared_error = 0.472\nsamples = 217\nvalue = 11.868'),
Text(0.06963603124480638, 0.46875, 'X[47] <= 0.184\nsquared_error = 8.407\nsamples = 3\nvalue = 9.706'),
Text(0.06930363968755193, 0.40625, 'squared_error = 0.0\nsamples = 1\nvalue = 5.617'),
Text(0.06996842280206082, 0.40625, 'X[0] <= 26534.602\nsquared_error = 0.069\nsamples = 2\nvalue = 11.751'),
Text(0.06963603124480638, 0.34375, 'squared_error = 0.0\nsamples = 1\nvalue = 12.014'),
Text(0.07030081435931528, 0.34375, 'squared_error = -0.0\nsamples = 1\nvalue = 11.488'),
Text(0.08492604287851088, 0.46875, 'X[1] <= 1525.0\nsquared_error = 0.295\nsamples = 214\nvalue = 11.899'),
Text(0.07570217716470001, 0.40625, 'X[22] <= 1.5\nsquared_error = 0.279\nsamples = 134\nvalue = 11.728'),
Text(0.07096559747382417, 0.34375, 'X[43] <= 0.013\nsquared_error = 0.241\nsamples = 100\nvalue = 11.854'),
Text(0.07063320591656971, 0.28125, 'squared_error = 0.0\nsamples = 1\nvalue = 10.463'),
Text(0.0712979890310786, 0.28125, 'X[44] <= 0.074\nsquared_error = 0.224\nsamples = 99\nvalue = 11.868'),
Text(0.06913744390892472, 0.21875, 'X[46] <= 0.388\nsquared_error = 0.305\nsamples = 7\nvalue = 11.36'),
Text(0.06847266079441582, 0.15625, 'X[54] <= 0.436\nsquared_error = 0.07\nsamples = 2\nvalue = 10.574'),
Text(0.06814026923716138, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 10.84'),
Text(0.06880505235167027, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 10.309'),
Text(0.06980222702343361, 0.15625, 'X[47] <= 0.771\nsquared_error = 0.053\nsamples = 5\nvalue = 11.674'),
Text(0.06946983546617916, 0.09375, 'squared_error = 0.0\nsamples = 2\nvalue = 11.408'),
Text(0.07013461858068805, 0.09375, 'X[46] <= 0.823\nsquared_error = 0.009\nsamples = 3\nvalue = 11.852'),
Text(0.06980222702343361, 0.03125, 'squared_error = 0.001\nsamples = 2\nvalue = 11.786'),
Text(0.0704670101379425, 0.03125, 'squared_error = -0.0\nsamples = 1\nvalue = 11.983'),
Text(0.0734585341532325, 0.21875, 'X[51] <= 0.929\nsquared_error = 0.196\nsamples = 92\nvalue = 11.907'),
Text(0.07212896792421472, 0.15625, 'X[54] <= 0.059\nsquared_error = 0.19\nsamples = 86\nvalue = 11.941'),
Text(0.07146418480970583, 0.09375, 'X[61] <= 0.254\nsquared_error = 0.05\nsamples = 6\nvalue = 12.462'),
Text(0.07113179325245139, 0.03125, 'squared_error = 0.008\nsamples = 2\nvalue = 12.703'),
Text(0.07179657636696028, 0.03125, 'squared_error = 0.027\nsamples = 4\nvalue = 12.342'),
Text(0.07279375103872361, 0.09375, 'X[54] <= 0.094\nsquared_error = 0.178\nsamples = 80\nvalue = 11.902'),
Text(0.07246135948146917, 0.03125, 'squared_error = 0.108\nsamples = 3\nvalue = 11.259'),
Text(0.07312614259597806, 0.03125, 'squared_error = 0.164\nsamples = 77\nvalue = 11.927'),
Text(0.0747881003822503, 0.15625, 'X[53] <= 0.44\nsquared_error = 0.037\nsamples = 6\nvalue = 11.417'),
Text(0.07412331726774139, 0.09375, 'X[53] <= 0.267\nsquared_error = 0.011\nsamples = 2\nvalue = 11.186'),
Text(0.07379092571048695, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.29'),
Text(0.07445570882499584, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.082'),
Text(0.07545288349675919, 0.09375, 'X[49] <= 0.129\nsquared_error = 0.011\nsamples = 4\nvalue = 11.532'),
Text(0.07512049193950474, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.695'),
Text(0.07578527505401363, 0.03125, 'squared_error = 0.002\nsamples = 3\nvalue = 11.478'),
Text(0.08043875685557587, 0.34375, 'X[59] <= 0.536\nsquared_error = 0.206\nsamples = 34\nvalue = 11.358'),
Text(0.07736413495097225, 0.28125, 'X[0] <= 13750.0\nsquared_error = 0.164\nsamples = 12\nvalue = 10.999'),
Text(0.07611766661126808, 0.21875, 'X[53] <= 0.323\nsquared_error = 0.049\nsamples = 3\nvalue = 11.527'),
Text(0.07578527505401363, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 11.225'),
Text(0.07645005816852252, 0.15625, 'X[46] <= 0.686\nsquared_error = 0.004\nsamples = 2\nvalue = 11.678'),
Text(0.07611766661126808, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.744'),
Text(0.07678244972577697, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 11.613'),
Text(0.07861060329067641, 0.21875, 'X[46] <= 0.38\nsquared_error = 0.079\nsamples = 9\nvalue = 10.824'),
Text(0.0777796243975403, 0.15625, 'X[20] <= 1.5\nsquared_error = 0.035\nsamples = 2\nvalue = 10.409'),
Text(0.07744723284028586, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 10.222'),
Text(0.07811201595479475, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 10.597'),
Text(0.07944158218381253, 0.15625, 'X[2] <= 1972.5\nsquared_error = 0.029\nsamples = 7\nvalue = 10.942'),
Text(0.07877679906930364, 0.09375, 'X[57] <= 0.741\nsquared_error = 0.011\nsamples = 2\nvalue = 11.186'),
Text(0.07844440751204919, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.29'),
Text(0.07910919062655808, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.082'),
Text(0.08010636529832142, 0.09375, 'X[38] <= 1.5\nsquared_error = 0.002\nsamples = 5\nvalue = 10.844'),
Text(0.07977397374106698, 0.03125, 'squared_error = 0.001\nsamples = 3\nvalue = 10.878'),
Text(0.08043875685557587, 0.03125, 'squared_error = 0.001\nsamples = 2\nvalue = 10.794'),
Text(0.08351337876017949, 0.28125, 'X[57] <= 0.216\nsquared_error = 0.121\nsamples = 22\nvalue = 11.554'),
Text(0.08176832308459366, 0.21875, 'X[48] <= 0.528\nsquared_error = 0.144\nsamples = 4\nvalue = 11.127'),
Text(0.08110353997008476, 0.15625, 'X[59] <= 0.71\nsquared_error = 0.046\nsamples = 2\nvalue = 11.439'),
Text(0.08077114841283031, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.225'),
Text(0.0814359315273392, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.653'),
Text(0.08243310619910255, 0.15625, 'X[60] <= 0.718\nsquared_error = 0.048\nsamples = 2\nvalue = 10.816'),
Text(0.0821007146418481, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 10.597'),
Text(0.08276549775635698, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 11.035'),
Text(0.08525843443576533, 0.21875, 'X[46] <= 0.793\nsquared_error = 0.066\nsamples = 18\nvalue = 11.649'),
Text(0.08409506398537477, 0.15625, 'X[51] <= 0.547\nsquared_error = 0.045\nsamples = 15\nvalue = 11.723'),
Text(0.08343028087086587, 0.09375, 'X[54] <= 0.426\nsquared_error = 0.029\nsamples = 10\nvalue = 11.613'),
Text(0.08309788931361144, 0.03125, 'squared_error = 0.012\nsamples = 5\nvalue = 11.468'),
Text(0.08376267242812033, 0.03125, 'squared_error = 0.004\nsamples = 5\nvalue = 11.758'),
Text(0.08475984709988366, 0.09375, 'X[60] <= 0.424\nsquared_error = 0.003\nsamples = 5\nvalue = 11.943'),
Text(0.08442745554262922, 0.03125, 'squared_error = 0.001\nsamples = 3\nvalue = 11.983'),
Text(0.08509223865713811, 0.03125, 'squared_error = 0.001\nsamples = 2\nvalue = 11.884'),
Text(0.08642180488615589, 0.15625, 'X[50] <= 0.412\nsquared_error = 0.009\nsamples = 3\nvalue = 11.277'),
Text(0.08608941332890145, 0.09375, 'X[62] <= 0.869\nsquared_error = 0.002\nsamples = 2\nvalue = 11.337'),
Text(0.085757021771647, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.29'),
Text(0.08642180488615589, 0.03125, 'squared_error = -0.0\nsamples = 1\nvalue = 11.385'),
Text(0.08675419644341034, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 11.156'),
Text(0.09414990859232175, 0.40625, 'X[2] <= 1935.0\nsquared_error = 0.191\nsamples = 80\nvalue = 12.185'),
Text(0.09016120990526841, 0.34375, 'X[53] <= 0.561\nsquared_error = 0.096\nsamples = 11\nvalue = 12.626'),
Text(0.08924713312281868, 0.28125, 'X[51] <= 0.872\nsquared_error = 0.059\nsamples = 8\nvalue = 12.489'),
Text(0.08841615422968256, 0.21875, 'X[46] <= 0.631\nsquared_error = 0.017\nsamples = 6\nvalue = 12.614'),
Text(0.08775137111517367, 0.15625, 'X[58] <= 0.778\nsquared_error = 0.0\nsamples = 2\nvalue = 12.78'),
Text(0.08741897955791923, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 12.794'),
Text(0.08808376267242812, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 12.766'),
Text(0.08908093734419145, 0.15625, 'X[43] <= 0.585\nsquared_error = 0.004\nsamples = 4\nvalue = 12.531'),
Text(0.08874854578693701, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 12.429'),
Text(0.0894133289014459, 0.09375, 'X[45] <= 0.569\nsquared_error = 0.001\nsamples = 3\nvalue = 12.566'),
Text(0.08908093734419145, 0.03125, 'squared_error = 0.0\nsamples = 2\nvalue = 12.543'),
Text(0.08974572045870034, 0.03125, 'squared_error = -0.0\nsamples = 1\nvalue = 12.612'),
Text(0.0900781120159548, 0.21875, 'X[46] <= 0.576\nsquared_error = 0.0\nsamples = 2\nvalue = 12.114'),
Text(0.08974572045870034, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 12.101'),
Text(0.09041050357320925, 0.15625, 'squared_error = -0.0\nsamples = 1\nvalue = 12.128'),
Text(0.09107528668771814, 0.28125, 'X[50] <= 0.556\nsquared_error = 0.011\nsamples = 3\nvalue = 12.99'),
Text(0.09074289513046369, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 12.848'),
Text(0.09140767824497258, 0.21875, 'X[41] <= 0.5\nsquared_error = 0.002\nsamples = 2\nvalue = 13.062'),
Text(0.09107528668771814, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 13.106'),
Text(0.09174006980222703, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 13.017'),
Text(0.09813860727937511, 0.34375, 'X[29] <= 1.5\nsquared_error = 0.17\nsamples = 69\nvalue = 12.114'),
Text(0.09489778959614426, 0.28125, 'X[46] <= 0.442\nsquared_error = 0.149\nsamples = 58\nvalue = 12.039'),
Text(0.09323583180987204, 0.21875, 'X[51] <= 0.879\nsquared_error = 0.119\nsamples = 26\nvalue = 11.852'),
Text(0.09240485291673592, 0.15625, 'X[58] <= 0.604\nsquared_error = 0.091\nsamples = 24\nvalue = 11.905'),
Text(0.09174006980222703, 0.09375, 'X[59] <= 0.565\nsquared_error = 0.03\nsamples = 12\nvalue = 12.078'),
Text(0.09140767824497258, 0.03125, 'squared_error = 0.009\nsamples = 5\nvalue = 11.914'),
Text(0.09207246135948147, 0.03125, 'squared_error = 0.012\nsamples = 7\nvalue = 12.195'),
Text(0.09306963603124481, 0.09375, 'X[55] <= 0.739\nsquared_error = 0.093\nsamples = 12\nvalue = 11.733'),
Text(0.09273724447399036, 0.03125, 'squared_error = 0.052\nsamples = 10\nvalue = 11.635'),
Text(0.09340202758849925, 0.03125, 'squared_error = 0.011\nsamples = 2\nvalue = 12.221'),
Text(0.09406681070300814, 0.15625, 'X[4] <= 2.5\nsquared_error = 0.018\nsamples = 2\nvalue = 11.216'),
Text(0.0937344191457537, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.082'),
Text(0.09439920226026259, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.35'),
Text(0.09655974738241649, 0.21875, 'X[0] <= 12100.0\nsquared_error = 0.122\nsamples = 32\nvalue = 12.19'),
Text(0.09539637693202592, 0.15625, 'X[49] <= 0.187\nsquared_error = 0.118\nsamples = 21\nvalue = 12.064'),
Text(0.09506398537477148, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 12.948'),
Text(0.09572876848928037, 0.09375, 'X[45] <= 0.989\nsquared_error = 0.083\nsamples = 20\nvalue = 12.02'),
Text(0.09539637693202592, 0.03125, 'squared_error = 0.052\nsamples = 19\nvalue = 12.062'),
Text(0.09606116004653482, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.225'),
Text(0.09772311783280704, 0.15625, 'X[48] <= 0.336\nsquared_error = 0.04\nsamples = 11\nvalue = 12.432'),
Text(0.09705833471829815, 0.09375, 'X[42] <= -2.0\nsquared_error = 0.001\nsamples = 2\nvalue = 12.066'),
Text(0.09672594316104371, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 12.101'),
Text(0.0973907262755526, 0.03125, 'squared_error = -0.0\nsamples = 1\nvalue = 12.032'),
Text(0.09838790094731593, 0.09375, 'X[50] <= 0.41\nsquared_error = 0.012\nsamples = 9\nvalue = 12.513'),
Text(0.0980555093900615, 0.03125, 'squared_error = 0.003\nsamples = 5\nvalue = 12.422'),
Text(0.09872029250457039, 0.03125, 'squared_error = 0.001\nsamples = 4\nvalue = 12.627'),
Text(0.10137942496260595, 0.28125, 'X[50] <= 0.558\nsquared_error = 0.093\nsamples = 11\nvalue = 12.512'),
Text(0.10004985873358817, 0.21875, 'X[46] <= 0.319\nsquared_error = 0.008\nsamples = 5\nvalue = 12.26'),
Text(0.09938507561907928, 0.15625, 'X[41] <= 0.5\nsquared_error = 0.0\nsamples = 2\nvalue = 12.357'),
Text(0.09905268406182482, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 12.346'),
Text(0.09971746717633372, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 12.367'),
Text(0.10071464184809706, 0.15625, 'X[32] <= 0.5\nsquared_error = 0.003\nsamples = 3\nvalue = 12.196'),
Text(0.1003822502908426, 0.09375, 'X[56] <= 0.603\nsquared_error = 0.001\nsamples = 2\nvalue = 12.23'),
Text(0.10004985873358817, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 12.255'),
Text(0.10071464184809706, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 12.206'),
Text(0.10104703340535151, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 12.128'),
Text(0.10270899119162373, 0.21875, 'X[32] <= 0.5\nsquared_error = 0.067\nsamples = 6\nvalue = 12.721'),
Text(0.10204420807711484, 0.15625, 'X[56] <= 0.08\nsquared_error = 0.006\nsamples = 4\nvalue = 12.897'),
Text(0.1017118165198604, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 12.766'),
Text(0.10237659963436929, 0.09375, 'X[52] <= 0.175\nsquared_error = 0.001\nsamples = 3\nvalue = 12.941'),
Text(0.10204420807711484, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 12.899'),
Text(0.10270899119162373, 0.03125, 'squared_error = 0.0\nsamples = 2\nvalue = 12.962'),
Text(0.10337377430613262, 0.15625, 'X[36] <= 0.761\nsquared_error = 0.002\nsamples = 2\nvalue = 12.368'),
Text(0.10304138274887818, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 12.324'),
Text(0.10370616586338707, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 12.413'),
Text(0.13297350216054513, 0.71875, 'X[30] <= 0.5\nsquared_error = 0.754\nsamples = 2413\nvalue = 11.219'),
Text(0.13264111060329067, 0.65625, 'squared_error = 0.0\nsamples = 1\nvalue = 0.0'),
Text(0.13330589371779958, 0.65625, 'X[1] <= 707.5\nsquared_error = 0.702\nsamples = 2412\nvalue = 11.223'),
Text(0.10819345188632208, 0.59375, 'X[57] <= 0.011\nsquared_error = 3.204\nsamples = 98\nvalue = 10.523'),
Text(0.10786106032906764, 0.53125, 'squared_error = 0.0\nsamples = 1\nvalue = 0.0'),
Text(0.10852584344357653, 0.53125, 'X[60] <= 0.97\nsquared_error = 2.083\nsamples = 97\nvalue = 10.631'),
Text(0.10786106032906764, 0.46875, 'X[55] <= 0.037\nsquared_error = 0.924\nsamples = 95\nvalue = 10.745'),
Text(0.10752866877181319, 0.40625, 'squared_error = 0.0\nsamples = 1\nvalue = 6.215'),
Text(0.10819345188632208, 0.40625, 'X[49] <= 0.067\nsquared_error = 0.714\nsamples = 94\nvalue = 10.793'),
Text(0.10437094897789596, 0.34375, 'X[35] <= -2.5\nsquared_error = 3.498\nsamples = 4\nvalue = 9.189'),
Text(0.10403855742064151, 0.28125, 'X[50] <= 0.184\nsquared_error = 0.73\nsamples = 3\nvalue = 10.181'),
Text(0.10370616586338707, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 11.29'),
Text(0.10437094897789596, 0.21875, 'X[45] <= 0.611\nsquared_error = 0.173\nsamples = 2\nvalue = 9.627'),
Text(0.10403855742064151, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 10.043'),
Text(0.1047033405351504, 0.15625, 'squared_error = -0.0\nsamples = 1\nvalue = 9.21'),
Text(0.1047033405351504, 0.28125, 'squared_error = -0.0\nsamples = 1\nvalue = 6.215'),
Text(0.11201595479474821, 0.34375, 'X[50] <= 0.556\nsquared_error = 0.471\nsamples = 90\nvalue = 10.864'),
Text(0.1082765497756357, 0.28125, 'X[1] <= 315.0\nsquared_error = 0.317\nsamples = 62\nvalue = 11.077'),
Text(0.10636529832142264, 0.21875, 'X[41] <= 0.5\nsquared_error = 0.237\nsamples = 9\nvalue = 11.66'),
Text(0.10536812364965929, 0.15625, 'X[8] <= 2.5\nsquared_error = 0.123\nsamples = 4\nvalue = 12.091'),
Text(0.10503573209240485, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.513'),
Text(0.10570051520691374, 0.09375, 'X[2] <= 1970.0\nsquared_error = 0.015\nsamples = 3\nvalue = 12.283'),
Text(0.10536812364965929, 0.03125, 'squared_error = 0.005\nsamples = 2\nvalue = 12.361'),
Text(0.10603290676416818, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 12.128'),
Text(0.10736247299318598, 0.15625, 'X[9] <= 5.5\nsquared_error = 0.061\nsamples = 5\nvalue = 11.315'),
Text(0.10703008143593153, 0.09375, 'X[0] <= 2900.0\nsquared_error = 0.01\nsamples = 4\nvalue = 11.2'),
Text(0.10669768987867709, 0.03125, 'squared_error = 0.001\nsamples = 2\nvalue = 11.112'),
Text(0.10736247299318598, 0.03125, 'squared_error = 0.004\nsamples = 2\nvalue = 11.288'),
Text(0.10769486455044042, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.775'),
Text(0.11018780122984877, 0.21875, 'X[34] <= 2.654\nsquared_error = 0.263\nsamples = 53\nvalue = 10.978'),
Text(0.1090244307794582, 0.15625, 'X[56] <= 0.039\nsquared_error = 0.223\nsamples = 50\nvalue = 11.028'),
Text(0.10835964766494931, 0.09375, 'X[52] <= 0.863\nsquared_error = 0.035\nsamples = 2\nvalue = 10.089'),
Text(0.10802725610769487, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 9.903'),
Text(0.10869203922220376, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 10.275'),
Text(0.10968921389396709, 0.09375, 'X[61] <= 0.115\nsquared_error = 0.193\nsamples = 48\nvalue = 11.067'),
Text(0.10935682233671265, 0.03125, 'squared_error = 0.027\nsamples = 7\nvalue = 10.649'),
Text(0.11002160545122154, 0.03125, 'squared_error = 0.186\nsamples = 41\nvalue = 11.138'),
Text(0.11135117168023932, 0.15625, 'X[43] <= 0.437\nsquared_error = 0.201\nsamples = 3\nvalue = 10.152'),
Text(0.11101878012298487, 0.09375, 'X[45] <= 0.462\nsquared_error = 0.065\nsamples = 2\nvalue = 9.871'),
Text(0.11068638856573043, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 10.127'),
Text(0.11135117168023932, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 9.616'),
Text(0.11168356323749377, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 10.714'),
Text(0.11575535981386073, 0.28125, 'X[2] <= 1955.0\nsquared_error = 0.488\nsamples = 28\nvalue = 10.392'),
Text(0.11417649991690211, 0.21875, 'X[58] <= 0.821\nsquared_error = 0.178\nsamples = 22\nvalue = 10.633'),
Text(0.11301312946651156, 0.15625, 'X[55] <= 0.893\nsquared_error = 0.101\nsamples = 18\nvalue = 10.509'),
Text(0.11234834635200266, 0.09375, 'X[50] <= 0.891\nsquared_error = 0.068\nsamples = 15\nvalue = 10.426'),
Text(0.11201595479474821, 0.03125, 'squared_error = 0.044\nsamples = 12\nvalue = 10.342'),
Text(0.1126807379092571, 0.03125, 'squared_error = 0.024\nsamples = 3\nvalue = 10.76'),
Text(0.11367791258102045, 0.09375, 'X[46] <= 0.382\nsquared_error = 0.06\nsamples = 3\nvalue = 10.922'),
Text(0.113345521023766, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 10.597'),
Text(0.11401030413827488, 0.03125, 'squared_error = 0.01\nsamples = 2\nvalue = 11.085'),
Text(0.11533987036729267, 0.15625, 'X[52] <= 0.344\nsquared_error = 0.14\nsamples = 4\nvalue = 11.195'),
Text(0.11500747881003823, 0.09375, 'X[62] <= 0.472\nsquared_error = 0.028\nsamples = 3\nvalue = 11.394'),
Text(0.11467508725278378, 0.03125, 'squared_error = 0.0\nsamples = 2\nvalue = 11.513'),
Text(0.11533987036729267, 0.03125, 'squared_error = -0.0\nsamples = 1\nvalue = 11.156'),
Text(0.11567226192454712, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 10.597'),
Text(0.11733421971081935, 0.21875, 'X[55] <= 0.795\nsquared_error = 0.632\nsamples = 6\nvalue = 9.509'),
Text(0.11666943659631045, 0.15625, 'X[2] <= 1989.5\nsquared_error = 0.029\nsamples = 4\nvalue = 10.061'),
Text(0.11633704503905601, 0.09375, 'squared_error = 0.0\nsamples = 2\nvalue = 9.903'),
Text(0.1170018281535649, 0.09375, 'X[48] <= 0.375\nsquared_error = 0.008\nsamples = 2\nvalue = 10.218'),
Text(0.11666943659631045, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 10.309'),
Text(0.11733421971081935, 0.03125, 'squared_error = -0.0\nsamples = 1\nvalue = 10.127'),
Text(0.11799900282532824, 0.15625, 'X[50] <= 0.685\nsquared_error = 0.012\nsamples = 2\nvalue = 8.406'),
Text(0.11766661126807379, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 8.294'),
Text(0.11833139438258268, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 8.517'),
Text(0.10919062655808542, 0.46875, 'X[44] <= 0.391\nsquared_error = 27.369\nsamples = 2\nvalue = 5.232'),
Text(0.10885823500083099, 0.40625, 'squared_error = 0.0\nsamples = 1\nvalue = 0.0'),
Text(0.10952301811533988, 0.40625, 'squared_error = 0.0\nsamples = 1\nvalue = 10.463'),
Text(0.15841833554927706, 0.59375, 'X[6] <= 1.5\nsquared_error = 0.575\nsamples = 2314\nvalue = 11.253'),
Text(0.1429854994183148, 0.53125, 'X[8] <= 1.5\nsquared_error = 0.462\nsamples = 1051\nvalue = 11.107'),
Text(0.12922760511882997, 0.46875, 'X[34] <= 2.154\nsquared_error = 0.75\nsamples = 71\nvalue = 10.484'),
Text(0.12310952301811534, 0.40625, 'X[55] <= 0.677\nsquared_error = 1.038\nsamples = 21\nvalue = 9.894'),
Text(0.12057503739405019, 0.34375, 'X[49] <= 0.274\nsquared_error = 0.717\nsamples = 15\nvalue = 9.46'),
Text(0.11866378593983713, 0.28125, 'X[51] <= 0.454\nsquared_error = 0.172\nsamples = 4\nvalue = 10.309'),
Text(0.11833139438258268, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 11.002'),
Text(0.11899617749709157, 0.21875, 'X[58] <= 0.737\nsquared_error = 0.016\nsamples = 3\nvalue = 10.078'),
Text(0.11866378593983713, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 9.903'),
Text(0.11932856905434602, 0.15625, 'X[61] <= 0.583\nsquared_error = 0.001\nsamples = 2\nvalue = 10.165'),
Text(0.11899617749709157, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 10.204'),
Text(0.11966096061160046, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 10.127'),
Text(0.12248628884826325, 0.28125, 'X[20] <= 1.5\nsquared_error = 0.558\nsamples = 11\nvalue = 9.152'),
Text(0.1213229183978727, 0.21875, 'X[61] <= 0.9\nsquared_error = 0.232\nsamples = 7\nvalue = 9.578'),
Text(0.1206581352833638, 0.15625, 'X[47] <= 0.904\nsquared_error = 0.026\nsamples = 5\nvalue = 9.291'),
Text(0.12032574372610935, 0.09375, 'squared_error = 0.0\nsamples = 4\nvalue = 9.21'),
Text(0.12099052684061824, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 9.616'),
Text(0.12198770151238159, 0.15625, 'X[61] <= 0.923\nsquared_error = 0.028\nsamples = 2\nvalue = 10.295'),
Text(0.12165530995512713, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 10.463'),
Text(0.12232009306963604, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 10.127'),
Text(0.12364965929865382, 0.21875, 'X[54] <= 0.655\nsquared_error = 0.253\nsamples = 4\nvalue = 8.406'),
Text(0.12331726774139937, 0.15625, 'X[62] <= 0.259\nsquared_error = 0.049\nsamples = 3\nvalue = 8.137'),
Text(0.12298487618414493, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 7.824'),
Text(0.12364965929865382, 0.09375, 'squared_error = 0.0\nsamples = 2\nvalue = 8.294'),
Text(0.12398205085590826, 0.15625, 'squared_error = -0.0\nsamples = 1\nvalue = 9.21'),
Text(0.12564400864218048, 0.34375, 'X[62] <= 0.629\nsquared_error = 0.196\nsamples = 6\nvalue = 10.978'),
Text(0.12464683397041715, 0.28125, 'X[41] <= 0.5\nsquared_error = 0.024\nsamples = 3\nvalue = 11.38'),
Text(0.12431444241316271, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 11.599'),
Text(0.1249792255276716, 0.21875, 'X[62] <= 0.294\nsquared_error = 0.0\nsamples = 2\nvalue = 11.271'),
Text(0.12464683397041715, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 11.252'),
Text(0.12531161708492605, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 11.29'),
Text(0.12664118331394383, 0.28125, 'X[43] <= 0.758\nsquared_error = 0.044\nsamples = 3\nvalue = 10.575'),
Text(0.12630879175668938, 0.21875, 'X[2] <= 1930.0\nsquared_error = 0.012\nsamples = 2\nvalue = 10.708'),
Text(0.12597640019943493, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 10.597'),
Text(0.12664118331394383, 0.15625, 'squared_error = -0.0\nsamples = 1\nvalue = 10.82'),
Text(0.12697357487119826, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 10.309'),
Text(0.13534568721954462, 0.40625, 'X[56] <= 0.57\nsquared_error = 0.422\nsamples = 50\nvalue = 10.732'),
Text(0.1315855077281037, 0.34375, 'X[45] <= 0.71\nsquared_error = 0.454\nsamples = 26\nvalue = 10.473'),
Text(0.12954960943992022, 0.28125, 'X[50] <= 0.499\nsquared_error = 0.328\nsamples = 20\nvalue = 10.676'),
Text(0.12797074954296161, 0.21875, 'X[59] <= 0.143\nsquared_error = 0.233\nsamples = 10\nvalue = 10.328'),
Text(0.1273059664284527, 0.15625, 'X[42] <= -2.0\nsquared_error = 0.12\nsamples = 2\nvalue = 9.557'),
Text(0.12697357487119826, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 9.21'),
Text(0.12763835798570716, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 9.903'),
Text(0.1286355326574705, 0.15625, 'X[49] <= 0.942\nsquared_error = 0.075\nsamples = 8\nvalue = 10.521'),
Text(0.12830314110021607, 0.09375, 'X[0] <= 2300.0\nsquared_error = 0.024\nsamples = 7\nvalue = 10.609'),
Text(0.12797074954296161, 0.03125, 'squared_error = 0.0\nsamples = 2\nvalue = 10.82'),
Text(0.1286355326574705, 0.03125, 'squared_error = 0.008\nsamples = 5\nvalue = 10.525'),
Text(0.12896792421472494, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 9.903'),
Text(0.13112846933687886, 0.21875, 'X[29] <= 0.5\nsquared_error = 0.181\nsamples = 10\nvalue = 11.023'),
Text(0.13029749044374273, 0.15625, 'X[41] <= 0.5\nsquared_error = 0.066\nsamples = 8\nvalue = 10.85'),
Text(0.12963270732923385, 0.09375, 'X[54] <= 0.248\nsquared_error = 0.01\nsamples = 6\nvalue = 10.983'),
Text(0.1293003157719794, 0.03125, 'squared_error = 0.002\nsamples = 2\nvalue = 10.867'),
Text(0.12996509888648827, 0.03125, 'squared_error = 0.004\nsamples = 4\nvalue = 11.041'),
Text(0.13096227355825163, 0.09375, 'X[52] <= 0.517\nsquared_error = 0.021\nsamples = 2\nvalue = 10.453'),
Text(0.13062988200099718, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 10.309'),
Text(0.13129466511550605, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 10.597'),
Text(0.13195944823001496, 0.15625, 'X[55] <= 0.927\nsquared_error = 0.041\nsamples = 2\nvalue = 11.716'),
Text(0.1316270566727605, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.918'),
Text(0.1322918397872694, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.513'),
Text(0.1336214060162872, 0.28125, 'X[54] <= 0.587\nsquared_error = 0.28\nsamples = 6\nvalue = 9.797'),
Text(0.1329566229017783, 0.21875, 'X[60] <= 0.341\nsquared_error = 0.037\nsamples = 3\nvalue = 9.345'),
Text(0.13262423134452384, 0.15625, 'squared_error = 0.0\nsamples = 2\nvalue = 9.21'),
Text(0.13328901445903274, 0.15625, 'squared_error = -0.0\nsamples = 1\nvalue = 9.616'),
Text(0.13428618913079607, 0.21875, 'X[0] <= 1175.0\nsquared_error = 0.117\nsamples = 3\nvalue = 10.248'),
Text(0.13395379757354164, 0.15625, 'X[15] <= 1.5\nsquared_error = 0.012\nsamples = 2\nvalue = 10.015'),
Text(0.1336214060162872, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 9.903'),
Text(0.13428618913079607, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 10.127'),
Text(0.13461858068805052, 0.15625, 'squared_error = -0.0\nsamples = 1\nvalue = 10.714'),
Text(0.13910586671098554, 0.34375, 'X[52] <= 0.438\nsquared_error = 0.235\nsamples = 24\nvalue = 11.012'),
Text(0.13644673425294998, 0.28125, 'X[60] <= 0.261\nsquared_error = 0.187\nsamples = 8\nvalue = 10.602'),
Text(0.13561575535981385, 0.21875, 'X[55] <= 0.192\nsquared_error = 0.005\nsamples = 3\nvalue = 11.085'),
Text(0.13528336380255943, 0.15625, 'X[4] <= 3.5\nsquared_error = 0.002\nsamples = 2\nvalue = 11.042'),
Text(0.13495097224530497, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.002'),
Text(0.13561575535981385, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.082'),
Text(0.1359481469170683, 0.15625, 'squared_error = -0.0\nsamples = 1\nvalue = 11.17'),
Text(0.13727771314608608, 0.21875, 'X[56] <= 0.821\nsquared_error = 0.073\nsamples = 5\nvalue = 10.313'),
Text(0.1366129300315772, 0.15625, 'X[46] <= 0.291\nsquared_error = 0.012\nsamples = 2\nvalue = 10.015'),
Text(0.13628053847432275, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 10.127'),
Text(0.13694532158883163, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 9.903'),
Text(0.137942496260595, 0.15625, 'X[60] <= 0.34\nsquared_error = 0.014\nsamples = 3\nvalue = 10.512'),
Text(0.13761010470334054, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 10.342'),
Text(0.13827488781784944, 0.09375, 'squared_error = -0.0\nsamples = 2\nvalue = 10.597'),
Text(0.1417649991690211, 0.28125, 'X[55] <= 0.249\nsquared_error = 0.134\nsamples = 16\nvalue = 11.217'),
Text(0.13993684560412165, 0.21875, 'X[51] <= 0.644\nsquared_error = 0.075\nsamples = 5\nvalue = 11.612'),
Text(0.13927206248961277, 0.15625, 'X[45] <= 0.818\nsquared_error = 0.038\nsamples = 3\nvalue = 11.426'),
Text(0.13893967093235832, 0.09375, 'X[15] <= 1.5\nsquared_error = 0.002\nsamples = 2\nvalue = 11.561'),
Text(0.13860727937510386, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.608'),
Text(0.13927206248961277, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.513'),
Text(0.13960445404686722, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 11.156'),
Text(0.14060162871863055, 0.15625, 'X[42] <= -2.0\nsquared_error = 0.0\nsamples = 2\nvalue = 11.891'),
Text(0.1402692371613761, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.871'),
Text(0.140934020275885, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 11.912'),
Text(0.14359315273392056, 0.21875, 'X[45] <= 0.327\nsquared_error = 0.058\nsamples = 11\nvalue = 11.038'),
Text(0.14226358650490278, 0.15625, 'X[1] <= 2066.402\nsquared_error = 0.018\nsamples = 4\nvalue = 11.31'),
Text(0.14159880339039388, 0.09375, 'X[29] <= 0.5\nsquared_error = 0.006\nsamples = 2\nvalue = 11.429'),
Text(0.14126641183313943, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.508'),
Text(0.14193119494764833, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.35'),
Text(0.14292836961941166, 0.09375, 'X[51] <= 0.677\nsquared_error = 0.001\nsamples = 2\nvalue = 11.191'),
Text(0.1425959780621572, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.225'),
Text(0.1432607611766661, 0.03125, 'squared_error = -0.0\nsamples = 1\nvalue = 11.156'),
Text(0.14492271896293835, 0.15625, 'X[49] <= 0.443\nsquared_error = 0.014\nsamples = 7\nvalue = 10.882'),
Text(0.14425793584842944, 0.09375, 'X[54] <= 0.072\nsquared_error = 0.002\nsamples = 4\nvalue = 10.793'),
Text(0.14392554429117502, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 10.714'),
Text(0.1445903274056839, 0.03125, 'squared_error = 0.0\nsamples = 3\nvalue = 10.82'),
Text(0.14558750207744722, 0.09375, 'X[54] <= 0.167\nsquared_error = 0.005\nsamples = 3\nvalue = 11.0'),
Text(0.1452551105201928, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 10.915'),
Text(0.14591989363470168, 0.03125, 'squared_error = 0.002\nsamples = 2\nvalue = 11.042'),
Text(0.15674339371779958, 0.46875, 'X[54] <= 0.001\nsquared_error = 0.411\nsamples = 980\nvalue = 11.153'),
Text(0.15641100216054513, 0.40625, 'squared_error = 0.0\nsamples = 1\nvalue = 6.908'),
Text(0.157075785275054, 0.40625, 'X[42] <= -2.5\nsquared_error = 0.393\nsamples = 979\nvalue = 11.157'),
Text(0.15244307794582018, 0.34375, 'X[8] <= 3.5\nsquared_error = 0.465\nsamples = 419\nvalue = 11.025'),
Text(0.1496592986538142, 0.28125, 'X[4] <= 4.5\nsquared_error = 0.437\nsamples = 392\nvalue = 10.983'),
Text(0.1480804387568556, 0.21875, 'X[0] <= 4100.0\nsquared_error = 0.412\nsamples = 384\nvalue = 10.966'),
Text(0.14724945986371946, 0.15625, 'X[46] <= 0.984\nsquared_error = 0.398\nsamples = 77\nvalue = 11.169'),
Text(0.146917068306465, 0.09375, 'X[50] <= 0.959\nsquared_error = 0.309\nsamples = 76\nvalue = 11.204'),
Text(0.14658467674921058, 0.03125, 'squared_error = 0.283\nsamples = 74\nvalue = 11.174'),
Text(0.14724945986371946, 0.03125, 'squared_error = 0.012\nsamples = 2\nvalue = 12.318'),
Text(0.1475818514209739, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 8.517'),
Text(0.1489114176499917, 0.15625, 'X[52] <= 0.141\nsquared_error = 0.402\nsamples = 307\nvalue = 10.915'),
Text(0.14824663453548279, 0.09375, 'X[2] <= 1919.5\nsquared_error = 0.524\nsamples = 42\nvalue = 10.606'),
Text(0.14791424297822836, 0.03125, 'squared_error = 0.352\nsamples = 4\nvalue = 9.544'),
Text(0.14857902609273724, 0.03125, 'squared_error = 0.411\nsamples = 38\nvalue = 10.717'),
Text(0.1495762007645006, 0.09375, 'X[4] <= 2.5\nsquared_error = 0.365\nsamples = 265\nvalue = 10.963'),
Text(0.14924380920724614, 0.03125, 'squared_error = 0.348\nsamples = 116\nvalue = 10.8'),
Text(0.14990859232175502, 0.03125, 'squared_error = 0.341\nsamples = 149\nvalue = 11.091'),
Text(0.1512381585507728, 0.21875, 'X[57] <= 0.097\nsquared_error = 0.985\nsamples = 8\nvalue = 11.799'),
Text(0.15090576699351838, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 14.036'),
Text(0.15157055010802725, 0.15625, 'X[47] <= 0.54\nsquared_error = 0.309\nsamples = 7\nvalue = 11.48'),
Text(0.15090576699351838, 0.09375, 'X[50] <= 0.554\nsquared_error = 0.051\nsamples = 5\nvalue = 11.81'),
Text(0.15057337543626392, 0.03125, 'squared_error = 0.015\nsamples = 3\nvalue = 11.976'),
Text(0.1512381585507728, 0.03125, 'squared_error = 0.002\nsamples = 2\nvalue = 11.561'),
Text(0.15223533322253616, 0.09375, 'X[62] <= 0.57\nsquared_error = 0.003\nsamples = 2\nvalue = 10.656'),
Text(0.1519029416652817, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 10.597'),
Text(0.15256772477979058, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 10.714'),
Text(0.15522685723782617, 0.28125, 'X[54] <= 0.858\nsquared_error = 0.458\nsamples = 27\nvalue = 11.641'),
Text(0.15456207412331727, 0.21875, 'X[1] <= 2316.402\nsquared_error = 0.298\nsamples = 24\nvalue = 11.784'),
Text(0.15422968256606281, 0.15625, 'X[2] <= 1955.0\nsquared_error = 0.212\nsamples = 23\nvalue = 11.848'),
Text(0.15356489945155394, 0.09375, 'X[47] <= 0.309\nsquared_error = 0.138\nsamples = 20\nvalue = 11.946'),
Text(0.15323250789429949, 0.03125, 'squared_error = 0.047\nsamples = 4\nvalue = 11.505'),
Text(0.1538972910088084, 0.03125, 'squared_error = 0.1\nsamples = 16\nvalue = 12.057'),
Text(0.15489446568057172, 0.09375, 'X[46] <= 0.148\nsquared_error = 0.216\nsamples = 3\nvalue = 11.195'),
Text(0.15456207412331727, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.849'),
Text(0.15522685723782617, 0.03125, 'squared_error = 0.002\nsamples = 2\nvalue = 10.867'),
Text(0.15489446568057172, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 10.309'),
Text(0.15589164035233505, 0.21875, 'X[48] <= 0.254\nsquared_error = 0.264\nsamples = 3\nvalue = 10.498'),
Text(0.1555592487950806, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 11.156'),
Text(0.1562240319095895, 0.15625, 'X[62] <= 0.338\nsquared_error = 0.07\nsamples = 2\nvalue = 10.169'),
Text(0.15589164035233505, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 10.434'),
Text(0.15655642346684395, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 9.903'),
Text(0.16170849260428785, 0.34375, 'X[29] <= 1.5\nsquared_error = 0.316\nsamples = 560\nvalue = 11.256'),
Text(0.15888316436762506, 0.28125, 'X[52] <= 0.004\nsquared_error = 0.298\nsamples = 555\nvalue = 11.248'),
Text(0.15722120658135283, 0.21875, 'X[45] <= 0.26\nsquared_error = 0.758\nsamples = 3\nvalue = 10.152'),
Text(0.15688881502409838, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 8.923'),
Text(0.15755359813860728, 0.15625, 'X[45] <= 0.52\nsquared_error = 0.003\nsamples = 2\nvalue = 10.767'),
Text(0.15722120658135283, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 10.714'),
Text(0.15788598969586173, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 10.82'),
Text(0.1605451221538973, 0.21875, 'X[0] <= 4850.0\nsquared_error = 0.289\nsamples = 552\nvalue = 11.254'),
Text(0.15921555592487951, 0.15625, 'X[43] <= 0.768\nsquared_error = 0.283\nsamples = 116\nvalue = 11.403'),
Text(0.1585507728103706, 0.09375, 'X[60] <= 0.935\nsquared_error = 0.252\nsamples = 89\nvalue = 11.313'),
Text(0.15821838125311616, 0.03125, 'squared_error = 0.238\nsamples = 86\nvalue = 11.285'),
Text(0.15888316436762506, 0.03125, 'squared_error = 0.019\nsamples = 3\nvalue = 12.091'),
Text(0.1598803390393884, 0.09375, 'X[48] <= 0.501\nsquared_error = 0.27\nsamples = 27\nvalue = 11.7'),
Text(0.15954794748213397, 0.03125, 'squared_error = 0.123\nsamples = 12\nvalue = 11.378'),
Text(0.16021273059664284, 0.03125, 'squared_error = 0.238\nsamples = 15\nvalue = 11.957'),
Text(0.16187468838291508, 0.15625, 'X[62] <= 0.985\nsquared_error = 0.283\nsamples = 436\nvalue = 11.214'),
Text(0.16120990526840617, 0.09375, 'X[52] <= 0.961\nsquared_error = 0.277\nsamples = 430\nvalue = 11.205'),
Text(0.16087751371115175, 0.03125, 'squared_error = 0.263\nsamples = 415\nvalue = 11.219'),
Text(0.16154229682566063, 0.03125, 'squared_error = 0.47\nsamples = 15\nvalue = 10.792'),
Text(0.16253947149742395, 0.09375, 'X[50] <= 0.463\nsquared_error = 0.282\nsamples = 6\nvalue = 11.891'),
Text(0.16220707994016953, 0.03125, 'squared_error = 0.019\nsamples = 4\nvalue = 11.548'),
Text(0.1628718630546784, 0.03125, 'squared_error = 0.104\nsamples = 2\nvalue = 12.577'),
Text(0.16453382084095064, 0.28125, 'X[58] <= 0.855\nsquared_error = 1.531\nsamples = 5\nvalue = 12.143'),
Text(0.1642014292836962, 0.21875, 'X[0] <= 15400.0\nsquared_error = 0.557\nsamples = 4\nvalue = 11.622'),
Text(0.1635366461691873, 0.15625, 'X[62] <= 0.779\nsquared_error = 0.003\nsamples = 2\nvalue = 10.876'),
Text(0.16320425461193286, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 10.933'),
Text(0.16386903772644174, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 10.82'),
Text(0.1648662123982051, 0.15625, 'X[53] <= 0.657\nsquared_error = 0.0\nsamples = 2\nvalue = 12.367'),
Text(0.16453382084095064, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 12.346'),
Text(0.16519860395545954, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 12.388'),
Text(0.1648662123982051, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 14.226'),
Text(0.1738511716802393, 0.53125, 'X[55] <= 0.003\nsquared_error = 0.636\nsamples = 1263\nvalue = 11.374'),
Text(0.1694365963104537, 0.46875, 'X[44] <= 0.838\nsquared_error = 23.012\nsamples = 4\nvalue = 8.307'),
Text(0.16910420475319926, 0.40625, 'X[52] <= 0.298\nsquared_error = 0.011\nsamples = 3\nvalue = 11.076'),
Text(0.16877181319594484, 0.34375, 'squared_error = -0.0\nsamples = 2\nvalue = 11.002'),
Text(0.1694365963104537, 0.34375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.225'),
Text(0.16976898786770817, 0.40625, 'squared_error = 0.0\nsamples = 1\nvalue = 0.0'),
Text(0.17826574705002493, 0.46875, 'X[29] <= 0.5\nsquared_error = 0.535\nsamples = 1259\nvalue = 11.384'),
Text(0.17354994183147748, 0.40625, 'X[51] <= 0.984\nsquared_error = 0.609\nsamples = 854\nvalue = 11.297'),
Text(0.17010137942496262, 0.34375, 'X[4] <= 2.5\nsquared_error = 0.453\nsamples = 844\nvalue = 11.313'),
Text(0.16802393219212233, 0.28125, 'X[51] <= 0.967\nsquared_error = 0.637\nsamples = 354\nvalue = 11.197'),
Text(0.16686056174173175, 0.21875, 'X[49] <= 0.995\nsquared_error = 0.505\nsamples = 349\nvalue = 11.217'),
Text(0.16652817018447733, 0.15625, 'X[0] <= 6225.0\nsquared_error = 0.483\nsamples = 348\nvalue = 11.208'),
Text(0.16586338706996842, 0.09375, 'X[31] <= 0.5\nsquared_error = 0.644\nsamples = 99\nvalue = 11.003'),
Text(0.16553099551271397, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 5.106'),
Text(0.16619577862722287, 0.03125, 'squared_error = 0.292\nsamples = 98\nvalue = 11.063'),
Text(0.1671929532989862, 0.09375, 'X[43] <= 0.909\nsquared_error = 0.396\nsamples = 249\nvalue = 11.29'),
Text(0.16686056174173175, 0.03125, 'squared_error = 0.342\nsamples = 226\nvalue = 11.241'),
Text(0.16752534485624065, 0.03125, 'squared_error = 0.671\nsamples = 23\nvalue = 11.77'),
Text(0.1671929532989862, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 14.063'),
Text(0.1691873026425129, 0.21875, 'X[60] <= 0.91\nsquared_error = 7.913\nsamples = 5\nvalue = 9.831'),
Text(0.16885491108525844, 0.15625, 'X[51] <= 0.982\nsquared_error = 0.153\nsamples = 4\nvalue = 11.227'),
Text(0.16852251952800398, 0.09375, 'X[54] <= 0.213\nsquared_error = 0.011\nsamples = 3\nvalue = 11.007'),
Text(0.16819012797074953, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.156'),
Text(0.16885491108525844, 0.03125, 'squared_error = 0.0\nsamples = 2\nvalue = 10.933'),
Text(0.1691873026425129, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.884'),
Text(0.1695196941997673, 0.15625, 'squared_error = -0.0\nsamples = 1\nvalue = 4.248'),
Text(0.1721788266578029, 0.28125, 'X[0] <= 126000.0\nsquared_error = 0.303\nsamples = 490\nvalue = 11.397'),
Text(0.17084926042878512, 0.21875, 'X[51] <= 0.124\nsquared_error = 0.255\nsamples = 455\nvalue = 11.37'),
Text(0.17018447731427622, 0.15625, 'X[45] <= 0.962\nsquared_error = 0.318\nsamples = 57\nvalue = 11.16'),
Text(0.16985208575702176, 0.09375, 'X[2] <= 1990.0\nsquared_error = 0.258\nsamples = 56\nvalue = 11.194'),
Text(0.1695196941997673, 0.03125, 'squared_error = 0.213\nsamples = 54\nvalue = 11.238'),
Text(0.17018447731427622, 0.03125, 'squared_error = 0.012\nsamples = 2\nvalue = 10.015'),
Text(0.17051686887153067, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 9.259'),
Text(0.171514043543294, 0.15625, 'X[59] <= 0.996\nsquared_error = 0.239\nsamples = 398\nvalue = 11.4'),
Text(0.17118165198603955, 0.09375, 'X[46] <= 0.105\nsquared_error = 0.221\nsamples = 397\nvalue = 11.393'),
Text(0.17084926042878512, 0.03125, 'squared_error = 0.186\nsamples = 45\nvalue = 11.123'),
Text(0.171514043543294, 0.03125, 'squared_error = 0.215\nsamples = 352\nvalue = 11.428'),
Text(0.17184643510054845, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 14.063'),
Text(0.17350839288682068, 0.21875, 'X[7] <= 1.5\nsquared_error = 0.799\nsamples = 35\nvalue = 11.752'),
Text(0.17284360977231178, 0.15625, 'X[58] <= 0.853\nsquared_error = 0.678\nsamples = 3\nvalue = 10.248'),
Text(0.17251121821505733, 0.09375, 'X[46] <= 0.456\nsquared_error = 0.21\nsamples = 2\nvalue = 10.767'),
Text(0.1721788266578029, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 10.309'),
Text(0.17284360977231178, 0.03125, 'squared_error = -0.0\nsamples = 1\nvalue = 11.225'),
Text(0.17317600132956623, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 9.21'),
Text(0.17417317600132956, 0.15625, 'X[57] <= 0.97\nsquared_error = 0.579\nsamples = 32\nvalue = 11.894'),
Text(0.1738407844440751, 0.09375, 'X[43] <= 0.612\nsquared_error = 0.416\nsamples = 31\nvalue = 11.818'),
Text(0.17350839288682068, 0.03125, 'squared_error = 0.369\nsamples = 19\nvalue = 11.571'),
Text(0.17417317600132956, 0.03125, 'squared_error = 0.241\nsamples = 12\nvalue = 12.209'),
Text(0.174505567558584, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 14.226'),
Text(0.17699850423799235, 0.34375, 'X[55] <= 0.872\nsquared_error = 11.808\nsamples = 10\nvalue = 9.911'),
Text(0.1766661126807379, 0.28125, 'X[47] <= 0.912\nsquared_error = 0.992\nsamples = 9\nvalue = 11.012'),
Text(0.17633372112348347, 0.21875, 'X[51] <= 0.992\nsquared_error = 0.241\nsamples = 8\nvalue = 11.324'),
Text(0.17550274223034734, 0.15625, 'X[61] <= 0.768\nsquared_error = 0.088\nsamples = 3\nvalue = 10.793'),
Text(0.17517035067309292, 0.09375, 'X[60] <= 0.778\nsquared_error = 0.0\nsamples = 2\nvalue = 11.002'),
Text(0.17483795911583846, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.002'),
Text(0.17550274223034734, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.002'),
Text(0.1758351337876018, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 10.373'),
Text(0.17716470001661958, 0.15625, 'X[52] <= 0.582\nsquared_error = 0.061\nsamples = 5\nvalue = 11.643'),
Text(0.1764999169021107, 0.09375, 'X[52] <= 0.459\nsquared_error = 0.02\nsamples = 3\nvalue = 11.462'),
Text(0.17616752534485625, 0.03125, 'squared_error = 0.007\nsamples = 2\nvalue = 11.376'),
Text(0.17683230845936512, 0.03125, 'squared_error = -0.0\nsamples = 1\nvalue = 11.635'),
Text(0.17782948313112848, 0.09375, 'X[52] <= 0.847\nsquared_error = 0.0\nsamples = 2\nvalue = 11.915'),
Text(0.17749709157387403, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.912'),
Text(0.1781618746883829, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.918'),
Text(0.17699850423799235, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 8.517'),
Text(0.1773308957952468, 0.28125, 'squared_error = 0.0\nsamples = 1\nvalue = 0.0'),
Text(0.18298155226857238, 0.40625, 'X[13] <= -7.5\nsquared_error = 0.33\nsamples = 405\nvalue = 11.568'),
Text(0.18264916071131793, 0.34375, 'squared_error = 0.0\nsamples = 1\nvalue = 5.106'),
Text(0.18331394382582683, 0.34375, 'X[9] <= 1.5\nsquared_error = 0.227\nsamples = 404\nvalue = 11.584'),
Text(0.17999002825328236, 0.28125, 'X[58] <= 0.964\nsquared_error = 0.299\nsamples = 34\nvalue = 12.039'),
Text(0.1796576366960279, 0.21875, 'X[50] <= 0.081\nsquared_error = 0.142\nsamples = 33\nvalue = 11.969'),
Text(0.1788266578028918, 0.15625, 'X[2] <= 1965.0\nsquared_error = 0.025\nsamples = 2\nvalue = 11.239'),
Text(0.17849426624563736, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.396'),
Text(0.17915904936014626, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.082'),
Text(0.18048861558916404, 0.15625, 'X[49] <= 0.138\nsquared_error = 0.114\nsamples = 31\nvalue = 12.016'),
Text(0.17982383247465514, 0.09375, 'X[62] <= 0.715\nsquared_error = 0.13\nsamples = 8\nvalue = 11.722'),
Text(0.17949144091740069, 0.03125, 'squared_error = 0.031\nsamples = 5\nvalue = 11.468'),
Text(0.1801562240319096, 0.03125, 'squared_error = 0.007\nsamples = 3\nvalue = 12.146'),
Text(0.18115339870367292, 0.09375, 'X[59] <= 0.286\nsquared_error = 0.067\nsamples = 23\nvalue = 12.118'),
Text(0.1808210071464185, 0.03125, 'squared_error = 0.044\nsamples = 4\nvalue = 12.431'),
Text(0.18148579026092737, 0.03125, 'squared_error = 0.048\nsamples = 19\nvalue = 12.052'),
Text(0.18032241981053682, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 14.344'),
Text(0.18663785939837127, 0.28125, 'X[8] <= 3.5\nsquared_error = 0.199\nsamples = 370\nvalue = 11.542'),
Text(0.18447731427621739, 0.21875, 'X[2] <= 1945.0\nsquared_error = 0.189\nsamples = 358\nvalue = 11.523'),
Text(0.1831477480471996, 0.15625, 'X[46] <= 0.134\nsquared_error = 0.268\nsamples = 95\nvalue = 11.375'),
Text(0.1824829649326907, 0.09375, 'X[62] <= 0.593\nsquared_error = 0.472\nsamples = 11\nvalue = 11.861'),
Text(0.18215057337543628, 0.03125, 'squared_error = 0.149\nsamples = 6\nvalue = 11.408'),
Text(0.18281535648994515, 0.03125, 'squared_error = 0.32\nsamples = 5\nvalue = 12.403'),
Text(0.18381253116170848, 0.09375, 'X[53] <= 0.996\nsquared_error = 0.206\nsamples = 84\nvalue = 11.311'),
Text(0.18348013960445406, 0.03125, 'squared_error = 0.184\nsamples = 83\nvalue = 11.328'),
Text(0.18414492271896293, 0.03125, 'squared_error = -0.0\nsamples = 1\nvalue = 9.903'),
Text(0.18580688050523517, 0.15625, 'X[0] <= 747657.0\nsquared_error = 0.15\nsamples = 263\nvalue = 11.577'),
Text(0.18514209739072626, 0.09375, 'X[0] <= 688910.0\nsquared_error = 0.142\nsamples = 261\nvalue = 11.569'),
Text(0.18480970583347184, 0.03125, 'squared_error = 0.132\nsamples = 259\nvalue = 11.577'),
Text(0.18547448894798071, 0.03125, 'squared_error = 0.392\nsamples = 2\nvalue = 10.53'),
Text(0.18647166361974407, 0.09375, 'X[58] <= 0.537\nsquared_error = 0.006\nsamples = 2\nvalue = 12.689'),
Text(0.18613927206248962, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 12.766'),
Text(0.1868040551769985, 0.03125, 'squared_error = -0.0\nsamples = 1\nvalue = 12.612'),
Text(0.18879840452052518, 0.21875, 'X[52] <= 0.789\nsquared_error = 0.188\nsamples = 12\nvalue = 12.09'),
Text(0.18846601296327073, 0.15625, 'X[51] <= 0.529\nsquared_error = 0.088\nsamples = 11\nvalue = 12.189'),
Text(0.18780122984876185, 0.09375, 'X[54] <= 0.509\nsquared_error = 0.059\nsamples = 6\nvalue = 12.377'),
Text(0.1874688382915074, 0.03125, 'squared_error = 0.006\nsamples = 4\nvalue = 12.544'),
Text(0.18813362140601628, 0.03125, 'squared_error = 0.0\nsamples = 2\nvalue = 12.044'),
Text(0.18913079607777963, 0.09375, 'X[56] <= 0.461\nsquared_error = 0.028\nsamples = 5\nvalue = 11.964'),
Text(0.18879840452052518, 0.03125, 'squared_error = 0.006\nsamples = 3\nvalue = 12.092'),
Text(0.18946318763503406, 0.03125, 'squared_error = 0.0\nsamples = 2\nvalue = 11.771'),
Text(0.18913079607777963, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 11.002'),
Text(0.30971557150573376, 0.78125, 'X[1] <= 1689.5\nsquared_error = 0.533\nsamples = 8841\nvalue = 11.854'),
Text(0.24529782802891806, 0.71875, 'X[62] <= 0.0\nsquared_error = 0.524\nsamples = 3241\nvalue = 11.677'),
Text(0.2278102667442247, 0.65625, 'X[60] <= 0.96\nsquared_error = 35.31\nsamples = 2\nvalue = 5.942'),
Text(0.22747787518697024, 0.59375, 'squared_error = 0.0\nsamples = 1\nvalue = 0.0'),
Text(0.22814265830147915, 0.59375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.884'),
Text(0.26278538931361145, 0.65625, 'X[19] <= 1.5\nsquared_error = 0.483\nsamples = 3239\nvalue = 11.68'),
Text(0.22880744141598802, 0.59375, 'X[29] <= 0.5\nsquared_error = 0.444\nsamples = 2852\nvalue = 11.711'),
Text(0.21402900116337045, 0.53125, 'X[1] <= 1383.0\nsquared_error = 0.421\nsamples = 2281\nvalue = 11.68'),
Text(0.20296659464849592, 0.46875, 'X[3] <= 2.5\nsquared_error = 0.404\nsamples = 984\nvalue = 11.597'),
Text(0.19627721455875022, 0.40625, 'X[52] <= 0.961\nsquared_error = 0.398\nsamples = 950\nvalue = 11.58'),
Text(0.19208077114841282, 0.34375, 'X[45] <= 0.003\nsquared_error = 0.287\nsamples = 913\nvalue = 11.597'),
Text(0.1902941665281702, 0.28125, 'X[62] <= 0.613\nsquared_error = 0.48\nsamples = 2\nvalue = 9.903'),
Text(0.18996177497091574, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 10.597'),
Text(0.19062655808542464, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 9.21'),
Text(0.19386737576865548, 0.28125, 'X[2] <= 1925.0\nsquared_error = 0.28\nsamples = 911\nvalue = 11.601'),
Text(0.19129134119993352, 0.21875, 'X[9] <= 1.5\nsquared_error = 0.242\nsamples = 35\nvalue = 11.936'),
Text(0.19012797074954296, 0.15625, 'X[59] <= 0.03\nsquared_error = 0.143\nsamples = 19\nvalue = 12.249'),
Text(0.1897955791922885, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.225'),
Text(0.19046036230679741, 0.09375, 'X[60] <= 0.114\nsquared_error = 0.09\nsamples = 18\nvalue = 12.305'),
Text(0.19012797074954296, 0.03125, 'squared_error = 0.039\nsamples = 3\nvalue = 12.755'),
Text(0.19079275386405184, 0.03125, 'squared_error = 0.051\nsamples = 15\nvalue = 12.215'),
Text(0.19245471165032407, 0.15625, 'X[45] <= 0.767\nsquared_error = 0.104\nsamples = 16\nvalue = 11.564'),
Text(0.1917899285358152, 0.09375, 'X[44] <= 0.339\nsquared_error = 0.053\nsamples = 11\nvalue = 11.705'),
Text(0.19145753697856074, 0.03125, 'squared_error = 0.011\nsamples = 3\nvalue = 11.439'),
Text(0.19212232009306965, 0.03125, 'squared_error = 0.032\nsamples = 8\nvalue = 11.805'),
Text(0.19311949476483298, 0.09375, 'X[57] <= 0.493\nsquared_error = 0.076\nsamples = 5\nvalue = 11.253'),
Text(0.19278710320757853, 0.03125, 'squared_error = 0.014\nsamples = 3\nvalue = 11.455'),
Text(0.19345188632208743, 0.03125, 'squared_error = 0.017\nsamples = 2\nvalue = 10.951'),
Text(0.19644341033737744, 0.21875, 'X[34] <= 2.154\nsquared_error = 0.277\nsamples = 876\nvalue = 11.588'),
Text(0.19511384410835964, 0.15625, 'X[49] <= 0.834\nsquared_error = 0.344\nsamples = 87\nvalue = 11.401'),
Text(0.19444906099385076, 0.09375, 'X[21] <= 1.5\nsquared_error = 0.325\nsamples = 72\nvalue = 11.313'),
Text(0.1941166694365963, 0.03125, 'squared_error = 0.237\nsamples = 67\nvalue = 11.389'),
Text(0.1947814525511052, 0.03125, 'squared_error = 0.384\nsamples = 5\nvalue = 10.296'),
Text(0.19577862722286854, 0.09375, 'X[61] <= 0.884\nsquared_error = 0.223\nsamples = 15\nvalue = 11.824'),
Text(0.1954462356656141, 0.03125, 'squared_error = 0.117\nsamples = 12\nvalue = 11.997'),
Text(0.196111018780123, 0.03125, 'squared_error = 0.053\nsamples = 3\nvalue = 11.136'),
Text(0.19777297656639523, 0.15625, 'X[0] <= 1225.0\nsquared_error = 0.265\nsamples = 789\nvalue = 11.608'),
Text(0.19710819345188632, 0.09375, 'X[46] <= 0.13\nsquared_error = 1.289\nsamples = 10\nvalue = 11.097'),
Text(0.19677580189463187, 0.03125, 'squared_error = 0.12\nsamples = 2\nvalue = 8.864'),
Text(0.19744058500914077, 0.03125, 'squared_error = 0.023\nsamples = 8\nvalue = 11.655'),
Text(0.1984377596809041, 0.09375, 'X[50] <= 0.026\nsquared_error = 0.249\nsamples = 779\nvalue = 11.615'),
Text(0.19810536812364965, 0.03125, 'squared_error = 0.56\nsamples = 19\nvalue = 11.244'),
Text(0.19877015123815855, 0.03125, 'squared_error = 0.238\nsamples = 760\nvalue = 11.624'),
Text(0.2004736579690876, 0.34375, 'X[52] <= 0.965\nsquared_error = 2.96\nsamples = 37\nvalue = 11.169'),
Text(0.199102542795413, 0.28125, 'X[60] <= 0.43\nsquared_error = 16.709\nsamples = 3\nvalue = 7.348'),
Text(0.19877015123815855, 0.21875, 'X[44] <= 0.292\nsquared_error = 0.362\nsamples = 2\nvalue = 10.218'),
Text(0.1984377596809041, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 10.82'),
Text(0.199102542795413, 0.15625, 'squared_error = -0.0\nsamples = 1\nvalue = 9.616'),
Text(0.19943493435266743, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 1.609'),
Text(0.20184477314276217, 0.28125, 'X[56] <= 0.147\nsquared_error = 0.346\nsamples = 34\nvalue = 11.506'),
Text(0.2004321090244308, 0.21875, 'X[5] <= 0.5\nsquared_error = 0.747\nsamples = 5\nvalue = 10.811'),
Text(0.19976732590992188, 0.15625, 'X[50] <= 0.261\nsquared_error = 0.25\nsamples = 3\nvalue = 11.442'),
Text(0.19943493435266743, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 10.82'),
Text(0.20009971746717634, 0.09375, 'X[1] <= 1100.0\nsquared_error = 0.085\nsamples = 2\nvalue = 11.753'),
Text(0.19976732590992188, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 12.044'),
Text(0.2004321090244308, 0.03125, 'squared_error = -0.0\nsamples = 1\nvalue = 11.462'),
Text(0.20109689213893966, 0.15625, 'X[15] <= 1.5\nsquared_error = 0.002\nsamples = 2\nvalue = 9.865'),
Text(0.2007645005816852, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 9.903'),
Text(0.20142928369619412, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 9.826'),
Text(0.20325743726109358, 0.21875, 'X[52] <= 0.966\nsquared_error = 0.179\nsamples = 29\nvalue = 11.626'),
Text(0.20242645836795745, 0.15625, 'X[62] <= 0.6\nsquared_error = 0.13\nsamples = 2\nvalue = 12.461'),
Text(0.20209406681070302, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 12.101'),
Text(0.2027588499252119, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 12.821'),
Text(0.20408841615422968, 0.15625, 'X[60] <= 0.379\nsquared_error = 0.127\nsamples = 27\nvalue = 11.564'),
Text(0.2034236330397208, 0.09375, 'X[53] <= 0.455\nsquared_error = 0.03\nsamples = 10\nvalue = 11.309'),
Text(0.20309124148246635, 0.03125, 'squared_error = 0.017\nsamples = 4\nvalue = 11.461'),
Text(0.20375602459697523, 0.03125, 'squared_error = 0.012\nsamples = 6\nvalue = 11.208'),
Text(0.20475319926873858, 0.09375, 'X[61] <= 0.147\nsquared_error = 0.123\nsamples = 17\nvalue = 11.714'),
Text(0.20442080771148413, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 10.82'),
Text(0.205085590825993, 0.03125, 'squared_error = 0.078\nsamples = 16\nvalue = 11.77'),
Text(0.20965597473824166, 0.40625, 'X[42] <= 1.5\nsquared_error = 0.349\nsamples = 34\nvalue = 12.051'),
Text(0.20757852750540137, 0.34375, 'X[56] <= 0.673\nsquared_error = 0.412\nsamples = 8\nvalue = 12.677'),
Text(0.20674754861226524, 0.28125, 'X[46] <= 0.769\nsquared_error = 0.138\nsamples = 6\nvalue = 12.383'),
Text(0.20608276549775636, 0.21875, 'X[47] <= 0.075\nsquared_error = 0.07\nsamples = 4\nvalue = 12.173'),
Text(0.2057503739405019, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 11.736'),
Text(0.2064151570550108, 0.15625, 'X[49] <= 0.788\nsquared_error = 0.009\nsamples = 3\nvalue = 12.318'),
Text(0.20608276549775636, 0.09375, 'X[42] <= -2.5\nsquared_error = 0.003\nsamples = 2\nvalue = 12.377'),
Text(0.2057503739405019, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 12.324'),
Text(0.2064151570550108, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 12.429'),
Text(0.20674754861226524, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 12.201'),
Text(0.20741233172677415, 0.21875, 'X[6] <= 4.0\nsquared_error = 0.009\nsamples = 2\nvalue = 12.803'),
Text(0.2070799401695197, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 12.707'),
Text(0.2077447232840286, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 12.899'),
Text(0.20840950639853748, 0.28125, 'X[45] <= 0.47\nsquared_error = 0.192\nsamples = 2\nvalue = 13.561'),
Text(0.20807711484128302, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 13.999'),
Text(0.20874189795579193, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 13.122'),
Text(0.21173342197108194, 0.34375, 'X[45] <= 0.165\nsquared_error = 0.171\nsamples = 26\nvalue = 11.859'),
Text(0.2100714641848097, 0.28125, 'X[59] <= 0.568\nsquared_error = 0.101\nsamples = 5\nvalue = 11.375'),
Text(0.2094066810703008, 0.21875, 'X[56] <= 0.237\nsquared_error = 0.028\nsamples = 3\nvalue = 11.613'),
Text(0.20907428951304638, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 11.385'),
Text(0.20973907262755526, 0.15625, 'X[50] <= 0.457\nsquared_error = 0.002\nsamples = 2\nvalue = 11.727'),
Text(0.2094066810703008, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.775'),
Text(0.2100714641848097, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.678'),
Text(0.21073624729931859, 0.21875, 'X[57] <= 0.703\nsquared_error = 0.0\nsamples = 2\nvalue = 11.018'),
Text(0.21040385574206416, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 11.035'),
Text(0.21106863885657304, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 11.002'),
Text(0.21339537975735418, 0.28125, 'X[32] <= 1.5\nsquared_error = 0.119\nsamples = 21\nvalue = 11.974'),
Text(0.21306298820009972, 0.21875, 'X[55] <= 0.604\nsquared_error = 0.08\nsamples = 20\nvalue = 11.928'),
Text(0.21173342197108194, 0.15625, 'X[47] <= 0.342\nsquared_error = 0.042\nsamples = 12\nvalue = 12.085'),
Text(0.21106863885657304, 0.09375, 'X[4] <= 3.5\nsquared_error = 0.013\nsamples = 5\nvalue = 12.249'),
Text(0.21073624729931859, 0.03125, 'squared_error = 0.002\nsamples = 2\nvalue = 12.114'),
Text(0.2114010304138275, 0.03125, 'squared_error = 0.0\nsamples = 3\nvalue = 12.339'),
Text(0.21239820508559082, 0.09375, 'X[49] <= 0.618\nsquared_error = 0.03\nsamples = 7\nvalue = 11.968'),
Text(0.21206581352833637, 0.03125, 'squared_error = 0.009\nsamples = 3\nvalue = 11.784'),
Text(0.21273059664284527, 0.03125, 'squared_error = 0.002\nsamples = 4\nvalue = 12.107'),
Text(0.2143925544291175, 0.15625, 'X[43] <= 0.657\nsquared_error = 0.044\nsamples = 8\nvalue = 11.691'),
Text(0.2137277713146086, 0.09375, 'X[60] <= 0.128\nsquared_error = 0.013\nsamples = 5\nvalue = 11.836'),
Text(0.21339537975735418, 0.03125, 'squared_error = 0.0\nsamples = 2\nvalue = 11.716'),
Text(0.21406016287186305, 0.03125, 'squared_error = 0.005\nsamples = 3\nvalue = 11.916'),
Text(0.21505733754362638, 0.09375, 'X[62] <= 0.4\nsquared_error = 0.004\nsamples = 3\nvalue = 11.45'),
Text(0.21472494598637196, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.535'),
Text(0.21538972910088083, 0.03125, 'squared_error = -0.0\nsamples = 2\nvalue = 11.408'),
Text(0.2137277713146086, 0.21875, 'squared_error = -0.0\nsamples = 1\nvalue = 12.899'),
Text(0.22509140767824498, 0.46875, 'X[53] <= 0.989\nsquared_error = 0.425\nsamples = 1297\nvalue = 11.743'),
Text(0.22216220707994017, 0.40625, 'X[59] <= 0.905\nsquared_error = 0.319\nsamples = 1281\nvalue = 11.753'),
Text(0.21979391723450226, 0.34375, 'X[47] <= 0.078\nsquared_error = 0.278\nsamples = 1164\nvalue = 11.774'),
Text(0.21821505733754362, 0.28125, 'X[1] <= 1660.0\nsquared_error = 1.127\nsamples = 85\nvalue = 11.538'),
Text(0.21788266578028917, 0.21875, 'X[51] <= 0.976\nsquared_error = 0.704\nsamples = 84\nvalue = 11.609'),
Text(0.21705168688715307, 0.15625, 'X[48] <= 0.85\nsquared_error = 0.253\nsamples = 82\nvalue = 11.671'),
Text(0.21638690377264416, 0.09375, 'X[53] <= 0.98\nsquared_error = 0.169\nsamples = 68\nvalue = 11.762'),
Text(0.21605451221538974, 0.03125, 'squared_error = 0.131\nsamples = 67\nvalue = 11.786'),
Text(0.21671929532989861, 0.03125, 'squared_error = -0.0\nsamples = 1\nvalue = 10.127'),
Text(0.21771647000166197, 0.09375, 'X[56] <= 0.554\nsquared_error = 0.432\nsamples = 14\nvalue = 11.232'),
Text(0.21738407844440752, 0.03125, 'squared_error = 0.057\nsamples = 8\nvalue = 11.706'),
Text(0.2180488615589164, 0.03125, 'squared_error = 0.235\nsamples = 6\nvalue = 10.601'),
Text(0.2187136446734253, 0.15625, 'X[62] <= 0.515\nsquared_error = 12.567\nsamples = 2\nvalue = 9.066'),
Text(0.21838125311617085, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 12.612'),
Text(0.21904603623067975, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 5.521'),
Text(0.21854744889479807, 0.21875, 'squared_error = -0.0\nsamples = 1\nvalue = 5.521'),
Text(0.22137277713146086, 0.28125, 'X[49] <= 0.997\nsquared_error = 0.206\nsamples = 1079\nvalue = 11.793'),
Text(0.22070799401695196, 0.21875, 'X[52] <= 0.997\nsquared_error = 0.2\nsamples = 1077\nvalue = 11.79'),
Text(0.22037560245969753, 0.15625, 'X[8] <= 3.5\nsquared_error = 0.196\nsamples = 1076\nvalue = 11.788'),
Text(0.21971081934518863, 0.09375, 'X[6] <= 1.5\nsquared_error = 0.188\nsamples = 944\nvalue = 11.768'),
Text(0.21937842778793418, 0.03125, 'squared_error = 0.209\nsamples = 163\nvalue = 11.644'),
Text(0.22004321090244308, 0.03125, 'squared_error = 0.179\nsamples = 781\nvalue = 11.794'),
Text(0.2210403855742064, 0.09375, 'X[51] <= 0.116\nsquared_error = 0.235\nsamples = 132\nvalue = 11.934'),
Text(0.22070799401695196, 0.03125, 'squared_error = 0.282\nsamples = 12\nvalue = 12.425'),
Text(0.22137277713146086, 0.03125, 'squared_error = 0.204\nsamples = 120\nvalue = 11.884'),
Text(0.2210403855742064, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 13.755'),
Text(0.22203756024596974, 0.21875, 'X[47] <= 0.57\nsquared_error = 1.464\nsamples = 2\nvalue = 13.224'),
Text(0.22170516868871532, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 12.014'),
Text(0.2223699518032242, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 14.433'),
Text(0.2245304969253781, 0.34375, 'X[28] <= 1.5\nsquared_error = 0.683\nsamples = 117\nvalue = 11.54'),
Text(0.22419810536812365, 0.28125, 'X[54] <= 0.997\nsquared_error = 0.373\nsamples = 116\nvalue = 11.592'),
Text(0.2238657138108692, 0.21875, 'X[44] <= 0.938\nsquared_error = 0.294\nsamples = 115\nvalue = 11.619'),
Text(0.2230347349177331, 0.15625, 'X[54] <= 0.089\nsquared_error = 0.234\nsamples = 113\nvalue = 11.652'),
Text(0.2223699518032242, 0.09375, 'X[61] <= 0.443\nsquared_error = 0.227\nsamples = 10\nvalue = 12.125'),
Text(0.22203756024596974, 0.03125, 'squared_error = 0.108\nsamples = 7\nvalue = 11.875'),
Text(0.22270234336047864, 0.03125, 'squared_error = 0.018\nsamples = 3\nvalue = 12.708'),
Text(0.22369951803224197, 0.09375, 'X[46] <= 0.942\nsquared_error = 0.211\nsamples = 103\nvalue = 11.606'),
Text(0.22336712647498755, 0.03125, 'squared_error = 0.193\nsamples = 97\nvalue = 11.57'),
Text(0.22403190958949643, 0.03125, 'squared_error = 0.14\nsamples = 6\nvalue = 12.187'),
Text(0.22469669270400533, 0.15625, 'X[59] <= 0.933\nsquared_error = 0.135\nsamples = 2\nvalue = 9.76'),
Text(0.22436430114675088, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 10.127'),
Text(0.22502908426125975, 0.09375, 'squared_error = 0.0\nsamples = 1\nvalue = 9.393'),
Text(0.2245304969253781, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 8.517'),
Text(0.22486288848263253, 0.28125, 'squared_error = -0.0\nsamples = 1\nvalue = 5.521'),
Text(0.22802060827654977, 0.40625, 'X[53] <= 0.99\nsquared_error = 8.246\nsamples = 16\nvalue = 10.945'),
Text(0.22768821671929532, 0.34375, 'squared_error = 0.0\nsamples = 1\nvalue = 0.0'),
Text(0.22835299983380422, 0.34375, 'X[43] <= 0.462\nsquared_error = 0.277\nsamples = 15\nvalue = 11.675'),
Text(0.22702343360478644, 0.28125, 'X[59] <= 0.468\nsquared_error = 0.091\nsamples = 6\nvalue = 12.191'),
Text(0.22635865049027754, 0.21875, 'X[47] <= 0.918\nsquared_error = 0.035\nsamples = 4\nvalue = 12.374'),
Text(0.2260262589330231, 0.15625, 'X[54] <= 0.317\nsquared_error = 0.002\nsamples = 3\nvalue = 12.268'),
Text(0.22569386737576866, 0.09375, 'X[46] <= 0.534\nsquared_error = 0.0\nsamples = 2\nvalue = 12.24'),
Text(0.2253614758185142, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 12.255'),
Text(0.2260262589330231, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 12.226'),
Text(0.22635865049027754, 0.09375, 'squared_error = -0.0\nsamples = 1\nvalue = 12.324'),
Text(0.226691042047532, 0.15625, 'squared_error = -0.0\nsamples = 1\nvalue = 12.692'),
Text(0.22768821671929532, 0.21875, 'X[48] <= 0.446\nsquared_error = 0.003\nsamples = 2\nvalue = 11.826'),
Text(0.2273558251620409, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 11.884'),
Text(0.22802060827654977, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 11.768'),
Text(0.229682566062822, 0.28125, 'X[52] <= 0.115\nsquared_error = 0.105\nsamples = 9\nvalue = 11.331'),
Text(0.22901778294831313, 0.21875, 'X[6] <= 4.0\nsquared_error = 0.042\nsamples = 2\nvalue = 11.839'),
Text(0.22868539139105867, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 12.044'),
Text(0.22935017450556755, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 11.635'),
Text(0.2303473491773309, 0.21875, 'X[42] <= -2.0\nsquared_error = 0.028\nsamples = 7\nvalue = 11.186'),
Text(0.23001495762007645, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 11.513'),
Text(0.23067974073458533, 0.15625, 'X[58] <= 0.197\nsquared_error = 0.011\nsamples = 6\nvalue = 11.131'),
Text(0.23001495762007645, 0.09375, 'X[1] <= 1552.5\nsquared_error = 0.0\nsamples = 3\nvalue = 11.234'),
Text(0.229682566062822, 0.03125, 'squared_error = 0.0\nsamples = 2\nvalue = 11.219'),
Text(0.2303473491773309, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.264'),
Text(0.23134452384909424, 0.09375, 'X[50] <= 0.374\nsquared_error = 0.001\nsamples = 3\nvalue = 11.029'),
Text(0.23101213229183978, 0.03125, 'squared_error = 0.0\nsamples = 1\nvalue = 11.082'),
Text(0.2316769154063487, 0.03125, 'squared_error = -0.0\nsamples = 2\nvalue = 11.002'),
Text(0.24358588166860562, 0.53125, 'X[60] <= 0.028\nsquared_error = 0.515\nsamples = 571\nvalue = 11.836'),
Text(0.23205085590825994, 0.46875, 'X[44] <= 0.203\nsquared_error = 6.361\nsamples = 14\nvalue = 10.979'),
Text(0.2303473491773309, 0.40625, 'X[0] <= 18375.0\nsquared_error = 10.398\nsamples = 3\nvalue = 7.141'),
Text(0.23001495762007645, 0.34375, 'squared_error = 0.0\nsamples = 1\nvalue = 11.695'),
Text(0.23067974073458533, 0.34375, 'X[55] <= 0.333\nsquared_error = 0.044\nsamples = 2\nvalue = 4.865'),
Text(0.2303473491773309, 0.28125, 'squared_error = 0.0\nsamples = 1\nvalue = 4.654'),
Text(0.23101213229183978, 0.28125, 'squared_error = 0.0\nsamples = 1\nvalue = 5.075'),
Text(0.23375436263918897, 0.40625, 'X[8] <= 2.5\nsquared_error = 0.147\nsamples = 11\nvalue = 12.026'),
Text(0.23234169852085756, 0.34375, 'X[51] <= 0.833\nsquared_error = 0.053\nsamples = 4\nvalue = 11.647'),
Text(0.2316769154063487, 0.28125, 'X[60] <= 0.005\nsquared_error = 0.015\nsamples = 2\nvalue = 11.859'),
Text(0.23134452384909424, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 11.983'),
Text(0.2320093069636031, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 11.736'),
Text(0.23300648163536647, 0.28125, 'X[62] <= 0.783\nsquared_error = 0.001\nsamples = 2\nvalue = 11.435'),
Text(0.23267409007811202, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 11.462'),
Text(0.2333388731926209, 0.21875, 'squared_error = 0.0\nsamples = 1\nvalue = 11.408'),
Text(0.23516702675752035, 0.34375, 'X[45] <= 0.258\nsquared_error = 0.072\nsamples = 7\nvalue = 12.243'),
Text(0.23433604786438425, 0.28125, 'X[58] <= 0.4\nsquared_error = 0.006\nsamples = 3\nvalue = 12.528'),
Text(0.2340036563071298, 0.21875, 'X[53] <= 0.561\nsquared_error = 0.001\nsamples = 2\nvalue = 12.577'),
Text(0.23367126474987535, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 12.612'),
Text(0.23433604786438425, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 12.543'),
Text(0.2346684394216387, 0.21875, 'squared_error = -0.0\nsamples = 1\nvalue = 12.429'),
Text(0.23599800565065648, 0.28125, 'X[47] <= 0.392\nsquared_error = 0.015\nsamples = 4\nvalue = 12.029'),
Text(0.23533322253614758, 0.21875, 'X[51] <= 0.712\nsquared_error = 0.001\nsamples = 2\nvalue = 11.918'),
Text(0.23500083097889313, 0.15625, 'squared_error = 0.0\nsamples = 1\nvalue = 11.884'),
...]

To reduce the complexity of the tree, we prune the tree: we collapse its leaves, permitting bias to increase but forcing variance to decrease until the desired trade-off is achieved. In rpart, this is done by considering a modified loss function that takes into account the number of terminal nodes (i.e., the number of regions in which the original data was partitioned). Somewhat heuristically, if we denote tree predictions by \(T(x)\) and its number of terminal nodes by \(|T|\), the modified regression problem can be written as:
The complexity of the tree is controlled by the scalar parameter \(c_p\), denoted as ccp_alpha in sklearn.tree.DecisionTreeRegressor. For each value of \(c_p\), we find the subtree that solves (2.4). Large values of \(c_p\) lead to aggressively pruned trees, which have more bias and less variance. Small values of \(c_p\) allow for deeper trees whose predictions can vary more wildly.
max_depth = []
mse_gini = []
for i in range(1,30):
dtree = DecisionTreeRegressor( max_depth=i, random_state = 0)
dtree.fit(x_train, y_train)
pred = dtree.predict(x_test)
mse_gini.append(mean_squared_error(y_test, pred))
max_depth.append(i)
d1 = pd.DataFrame({'acc_gini':pd.Series(mse_gini),'max_depth':pd.Series(max_depth)})
# visualizing changes in parameters
plt.figure(figsize=(18,5))
plt.plot('max_depth','acc_gini', data=d1, label='mse', marker="o")
plt.xlabel('max_depth')
plt.ylabel('mse')
plt.legend()
<matplotlib.legend.Legend at 0x1825a929760>
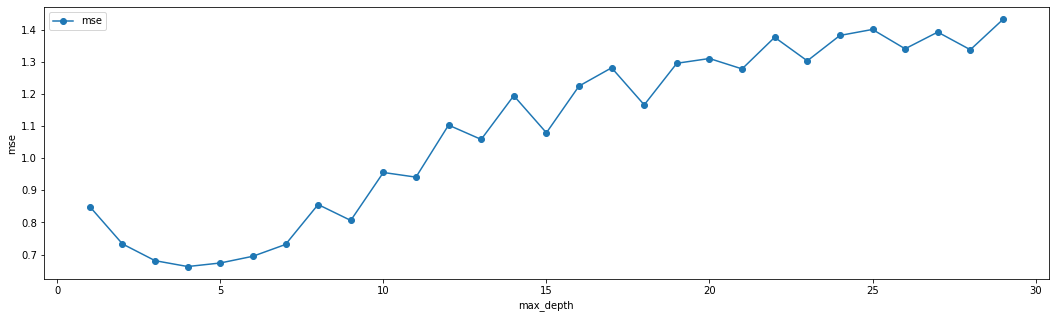
path = dt.cost_complexity_pruning_path(x_train,y_train)
alphas_dt = pd.Series(path['ccp_alphas'], name = "alphas")
# A function with a manual cross validation
def run_cross_validation_on_trees(X, y, tree_ccp, nfold=10):
cv_scores_list = []
cv_scores_mean = []
cv_scores_std = []
cp_table = []
cp_table_error = []
cp_table_std = []
cp_table_rel_error = []
# Num ob observations
nobs = y.shape[0]
# Define folds indices
list_1 = [*range(0, nfold, 1)]*nobs
sample = np.random.choice(nobs,nobs, replace=False).tolist()
foldid = [list_1[index] for index in sample]
# Create split function(similar to R)
def split(x, f):
count = max(f) + 1
return tuple( list(itertools.compress(x, (el == i for el in f))) for i in range(count) )
# Split observation indices into folds
list_2 = [*range(0, nobs, 1)]
I = split(list_2, foldid)
for i in tree_ccp:
dtree = DecisionTreeRegressor( ccp_alpha= i, random_state = 0)
# loop to save results
for b in range(0,len(I)):
# Split data - index to keep are in mask as booleans
include_idx = set(I[b]) #Here should go I[b] Set is more efficient, but doesn't reorder your elements if that is desireable
mask = np.array([(a in include_idx) for a in range(len(y))])
dtree.fit(X[~mask], Y[~mask])
pred = dtree.predict(X[mask])
xerror_fold = np.mean(np.power(Y[mask] - pred,2))
rel_error_fold = 1- r2_score(Y[mask], pred)
cv_scores_list.append(xerror_fold)
rel_error = np.mean(rel_error_fold)
xerror = np.mean(cv_scores_list)
xstd = np.std(cv_scores_list)
cp_table_rel_error.append(rel_error)
cp_table_error.append(xerror)
cp_table_std.append(xstd)
cp_table = pd.DataFrame([pd.Series(alphas_dt, name = "cp"), pd.Series(cp_table_rel_error, name = "rel error")
,pd.Series(cp_table_error, name = "xerror"),
pd.Series(cp_table_std, name = "xstd")]).T
return cp_table
sm_tree_ccp = alphas_dt[0:3]
cp_table = run_cross_validation_on_trees(XX, Y, sm_tree_ccp)
cp_table.head()
| cp | rel error | xerror | xstd | |
|---|---|---|---|---|
| 0 | 0.000000e+00 | 1.301711 | 1.304097 | 0.091112 |
| 1 | 7.067264e-19 | 1.301711 | 1.304097 | 0.091112 |
| 2 | 1.060090e-18 | 1.301711 | 1.304097 | 0.091112 |
| 3 | 1.413453e-18 | NaN | NaN | NaN |
| 4 | 1.413453e-18 | NaN | NaN | NaN |
def run_cross_validation_on_trees(X, y, tree_ccp, cv=5, scoring='neg_mean_squared_error'):
cv_scores_list = []
cv_scores_std = []
cv_scores_mean = []
MSE_scores = []
for ccp in tree_ccp:
tree_model = DecisionTreeRegressor(ccp_alpha= ccp, random_state=0)
cv_scores = -1*cross_val_score(tree_model, X, y, cv=cv, scoring= scoring)
cv_scores_list.append(cv_scores)
cv_scores_mean.append(cv_scores.mean())
cv_scores_std.append(cv_scores.std())
# MSE_scores.append(tree_model.fit(X, y).score(X, y))
cv_scores_mean = np.array(cv_scores_mean)
cv_scores_std = np.array(cv_scores_std)
# MSE_scores = np.array(MSE_scores)
return cv_scores_mean, cv_scores_std
# fitting trees
sm_tree_ccp = alphas_dt[:10] #it should run all alphas, but it takes too long
sm_cv_scores_mean, sm_cv_scores_std = run_cross_validation_on_trees(XX, Y, sm_tree_ccp)
sm_cv_scores_mean
array([1.32904969, 1.32904969, 1.32904969, 1.32904969, 1.32904969,
1.32904969, 1.32904969, 1.32904969, 1.32904969, 1.32904969])
cp_table = pd.DataFrame([pd.Series(alphas_dt, name = "cp"), pd.Series(sm_cv_scores_mean, name = "MSE"),
pd.Series(sm_cv_scores_std/math.sqrt(10), name = "xstd")]).T
cp_table
| cp | MSE | xstd | |
|---|---|---|---|
| 0 | 0.000000e+00 | 1.32905 | 0.035923 |
| 1 | 7.067264e-19 | 1.32905 | 0.035923 |
| 2 | 1.060090e-18 | 1.32905 | 0.035923 |
| 3 | 1.413453e-18 | 1.32905 | 0.035923 |
| 4 | 1.413453e-18 | 1.32905 | 0.035923 |
| ... | ... | ... | ... |
| 1725 | 1.361723e-02 | NaN | NaN |
| 1726 | 1.645619e-02 | NaN | NaN |
| 1727 | 3.639536e-02 | NaN | NaN |
| 1728 | 9.906067e-02 | NaN | NaN |
| 1729 | 1.475424e-01 | NaN | NaN |
1730 rows × 3 columns
mse_gini = []
for i in alphas_dt:
dtree = DecisionTreeRegressor( ccp_alpha=i, random_state = 0)
dtree.fit(x_train, y_train)
pred = dtree.predict(x_test)
mse_gini.append(mean_squared_error(y_test, pred))
d2 = pd.DataFrame({'acc_gini':pd.Series(mse_gini),'ccp_alphas':pd.Series(alphas_dt)})
#plt.style.context("dark_background")
# visualizing changes in parameters
plt.figure(figsize=(18,5), facecolor = "white")
plt.plot('ccp_alphas','acc_gini', data=d2, label='mse', marker="o", color='black')
#plt.gca().invert_xaxis()
#plt.xticks(np.arange(0, 0.15, step=0.01)) # Set label locations.
#plt.yticks(np.arange(0.5, 1.5, step=0.1)) # Set label locations.
plt.tick_params( axis='x', labelsize=15, length=0, labelrotation=0)
plt.tick_params( axis='y', labelsize=15, length=0, labelrotation=0)
plt.grid()
plt.xlabel('ccp_alphas', fontsize = 15)
plt.ylabel('mse', fontsize = 15)
plt.legend()
<matplotlib.legend.Legend at 0x1825da220d0>
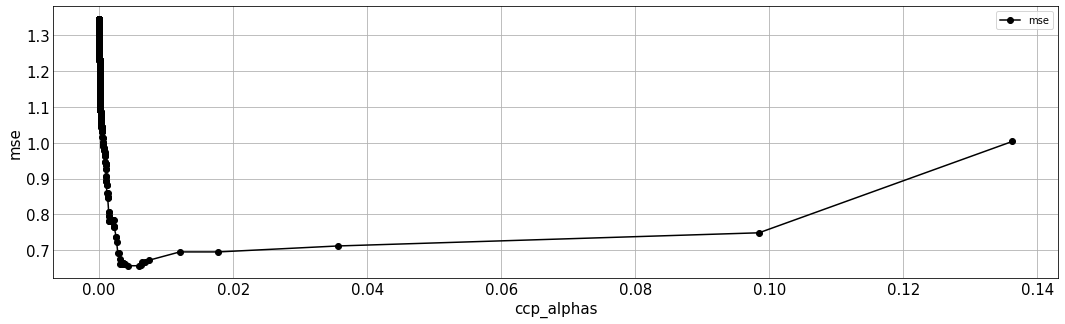
mse_dt = pd.Series(mse_gini, name = "mse")
filter_df = pd.DataFrame(data= [alphas_dt, mse_dt]).T
The following code retrieves the optimal parameter and prunes the tree. Here, instead of choosing the parameter that minimizes the mean-squared-error, we’re following another common heuristic: we will choose the most regularized model whose error is within one standard error of the minimum error.
best_max_depth = d1[d1["acc_gini"] == np.min(d1["acc_gini"])].iloc[0,1]
best_ccp = filter_df[filter_df["mse"] == np.min(filter_df["mse"]) ].iloc[0,0]
# Prune the tree
dt = DecisionTreeRegressor(ccp_alpha= best_ccp , max_depth= best_max_depth, random_state=0)
tree1 = dt.fit(x_train,y_train)
Plotting the pruned tree. See also the package rpart.plot for more advanced plotting capabilities.
from sklearn import tree
plt.figure(figsize=(18,5))
tree.plot_tree(dt, filled=True, rounded=True)
[Text(0.6764705882352942, 0.9, 'X[22] <= 3.5\nsquared_error = 0.955\nsamples = 20108\nvalue = 11.816'),
Text(0.47058823529411764, 0.7, 'X[1] <= 2436.5\nsquared_error = 0.77\nsamples = 19388\nvalue = 11.887'),
Text(0.23529411764705882, 0.5, 'X[3] <= 1.5\nsquared_error = 0.643\nsamples = 13926\nvalue = 11.687'),
Text(0.11764705882352941, 0.3, 'X[19] <= 1.5\nsquared_error = 0.713\nsamples = 5053\nvalue = 11.387'),
Text(0.058823529411764705, 0.1, 'squared_error = 0.622\nsamples = 2644\nvalue = 11.544'),
Text(0.17647058823529413, 0.1, 'squared_error = 0.755\nsamples = 2409\nvalue = 11.214'),
Text(0.35294117647058826, 0.3, 'X[1] <= 1691.5\nsquared_error = 0.523\nsamples = 8873\nvalue = 11.858'),
Text(0.29411764705882354, 0.1, 'squared_error = 0.496\nsamples = 3243\nvalue = 11.687'),
Text(0.4117647058823529, 0.1, 'squared_error = 0.512\nsamples = 5630\nvalue = 11.957'),
Text(0.7058823529411765, 0.5, 'X[3] <= 2.5\nsquared_error = 0.729\nsamples = 5462\nvalue = 12.398'),
Text(0.5882352941176471, 0.3, 'X[3] <= 1.5\nsquared_error = 0.665\nsamples = 2848\nvalue = 12.152'),
Text(0.5294117647058824, 0.1, 'squared_error = 1.095\nsamples = 340\nvalue = 11.594'),
Text(0.6470588235294118, 0.1, 'squared_error = 0.559\nsamples = 2508\nvalue = 12.228'),
Text(0.8235294117647058, 0.3, 'X[1] <= 3999.0\nsquared_error = 0.662\nsamples = 2614\nvalue = 12.665'),
Text(0.7647058823529411, 0.1, 'squared_error = 0.561\nsamples = 1666\nvalue = 12.497'),
Text(0.8823529411764706, 0.1, 'squared_error = 0.704\nsamples = 948\nvalue = 12.96'),
Text(0.8823529411764706, 0.7, 'X[12] <= 1.5\nsquared_error = 2.138\nsamples = 720\nvalue = 9.901'),
Text(0.8235294117647058, 0.5, 'squared_error = 2.31\nsamples = 429\nvalue = 9.423'),
Text(0.9411764705882353, 0.5, 'squared_error = 1.052\nsamples = 291\nvalue = 10.605')]

Finally, here’s how to extract predictions and mse estimates from the pruned tree.
# Retrieve predictions from pruned tre
y_pred = dt.predict(x_test)
# Compute mse for pruned tree (using cross-validated predictions)
mse = mean_squared_error(y_test, y_pred)
print("Tree MSE estimate:", mse)
Tree MSE estimate: 0.656562830536762
It’s often said that trees are “interpretable.” To some extent, that’s true – we can look at the tree and clearly visualize the mapping from inputs to prediction. This can be important in settings in which conveying how one got to a prediction is important. For example, if a decision tree were to be used for credit scoring, it would be easy to explain to a client how their credit was scored.
Beyond that, however, there are several reasons for not interpreting the obtained decision tree further. First, even though a tree may have used a particular variable for a split, that does not mean that it’s indeed an important variable: if two covariates are highly correlated, the tree may split on one variable but not the other, and there’s no guarantee which variables are relevant in the underlying data-generating process.
Similar to what we did for Lasso above, we can estimate the average value of each covariate per leaf. Although results are noisier here because there are many leaves, we see somewhat similar trends in that houses with higher predictions are also correlated with more bedrooms, bathrooms and room sizes.
from pandas import Series
from simple_colors import *
import statsmodels.api as sm
import statsmodels.formula.api as smf
from scipy.stats import norm
y_pred
# Number of leaves should equal the number of distinct prediction values.
# This should be okay for most applications, but if an exact answer is needed use
# predict.rpart.leaves from package treeCluster
num_leaves = len(pd.Series(y_pred).unique())
# Leaf membership, ordered by increasing prediction value
categ = pd.Categorical(y_pred, categories= np.sort(pd.unique(y_pred)))
leaf = categ.rename_categories(np.arange(1,len(categ.categories)+1))
# Looping over covariates
data1 = pd.DataFrame(data=x_test, columns= covariates)
data1["leaf"] = leaf
for var_name in covariates:
# Coefficients on linear regression of covariate on leaf
# are the average covariate value in each leaf.
# covariate ~ leaf.1 + ... + leaf.L
form2 = var_name + " ~ " + "0" + "+" + "leaf"
# Heteroskedasticity-robust standard errors
ols = smf.ols(formula=form2, data=data1).fit(cov_type = 'HC2').summary2().tables[1].iloc[:, 0:2].T
print(red(var_name, 'bold'),ols, "\n")
LOT leaf[1] leaf[2] leaf[3] leaf[4] \
Coef. 62147.992348 156095.016394 37918.059380 37963.609724
Std.Err. 9679.715527 18439.782886 3374.904533 3040.919277
leaf[5] leaf[6] leaf[7] leaf[8] \
Coef. 57460.902664 35800.336601 47309.306565 52027.215145
Std.Err. 11958.583936 2572.586333 2453.410031 3692.568525
leaf[9] leaf[10]
Coef. 49146.276086 75986.183034
Std.Err. 4299.266616 7573.937525
UNITSF leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] \
Coef. 1497.891661 1888.676869 1579.970803 1537.358397 5201.335526
Std.Err. 111.922106 130.153136 18.687591 15.776454 385.749500
leaf[6] leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 1360.202752 2075.217669 3612.324569 3129.419532 7927.140777
Std.Err. 5.905033 5.117509 72.067705 14.816769 210.685167
BUILT leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] \
Coef. 1981.613260 1987.591837 1948.011091 1957.886364 1952.697368
Std.Err. 1.037346 1.085556 0.603229 0.660465 2.026017
leaf[6] leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 1977.029689 1979.056555 1982.184950 1987.643741 1988.274272
Std.Err. 0.600677 0.469025 0.667451 0.754772 1.098346
BATHS leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 1.558011 2.013605 0.987061 0.999091 0.993421 2.040550
Std.Err. 0.039425 0.033421 0.003437 0.000909 0.006579 0.005408
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 2.143530 2.000000e+00 3.145805 3.674757
Std.Err. 0.008028 1.337784e-16 0.014074 0.038914
BEDRMS leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 2.502762 3.102041 2.705176 2.770909 3.171053 2.974656
Std.Err. 0.041180 0.050838 0.022705 0.021643 0.072172 0.016488
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 3.337618 3.617407 4.063274 4.495146
Std.Err. 0.013899 0.020535 0.026156 0.042161
DINING leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.232044 0.489796 0.488909 0.516364 0.723684 0.472122
Std.Err. 0.034266 0.042483 0.015702 0.015400 0.037569 0.013937
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.724936 0.853128 0.927098 1.004854
Std.Err. 0.010190 0.013337 0.015150 0.017182
METRO leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 6.309392 6.734694 4.272643 5.008182 4.361842 5.503983
Std.Err. 0.139132 0.098600 0.090002 0.083896 0.239370 0.068088
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 5.713796 6.013599 6.152682 6.361650
Std.Err. 0.049852 0.065963 0.075993 0.090116
CRACKS leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 1.911602 1.938776 1.910351 1.944545 1.927632 1.946416
Std.Err. 0.021159 0.019841 0.008689 0.006904 0.021085 0.006062
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 1.952871 1.962829 1.953232 1.970874
Std.Err. 0.004387 0.005699 0.007836 0.008295
REGION leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 2.867403 2.897959 2.459335 2.503636 2.519737 2.876901
Std.Err. 0.046622 0.047030 0.019717 0.023699 0.061191 0.017219
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 2.760069 2.694470 2.858322 2.781553
Std.Err. 0.013108 0.020404 0.023131 0.032994
METRO3 leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 1.878453 1.952381 1.641405 1.804545 1.598684 2.031861
Std.Err. 0.024355 0.017625 0.031286 0.034764 0.063490 0.040993
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 2.054841 2.128740 2.074278 2.247573
Std.Err. 0.030523 0.045094 0.048274 0.078698
PHONE leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.541436 0.564626 0.707948 0.750909 0.592105 0.743664
Std.Err. 0.143505 0.160974 0.047290 0.043139 0.145920 0.038788
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.682091 0.773345 0.669876 0.631068
Std.Err. 0.033012 0.041261 0.060200 0.085295
KITCHEN leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 1.000000e+00 1.020408 1.015712 1.007273 1.013158 1.006517
Std.Err. 6.620091e-17 0.011702 0.003782 0.002563 0.009273 0.002166
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 1.001714 1.000907 1.001376 1.002427
Std.Err. 0.000856 0.000907 0.001376 0.002427
MOBILTYP leaf[1] leaf[2] leaf[3] leaf[4] \
Coef. 1.000000e+00 2.000000e+00 -1.000000e+00 -1.000000e+00
Std.Err. 6.620091e-17 3.675308e-17 1.485765e-16 1.339588e-16
leaf[5] leaf[6] leaf[7] leaf[8] \
Coef. -1.000000e+00 -1.000000e+00 -1.000000e+00 -1.000000e+00
Std.Err. 1.806973e-17 1.314993e-16 1.333156e-16 6.688819e-17
leaf[9] leaf[10]
Coef. -1.000000e+00 -1.000000e+00
Std.Err. 1.318536e-16 1.095265e-17
WINTEROVEN leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 1.917127 1.850340 1.931608 1.937273 1.921053 1.940623
Std.Err. 0.051305 0.096221 0.017023 0.022029 0.066353 0.019016
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 1.949871 1.978241 1.986245 1.917476
Std.Err. 0.013986 0.012938 0.012454 0.040895
WINTERKESP leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 1.895028 1.809524 1.935305 1.926364 1.927632 1.934830
Std.Err. 0.052268 0.097175 0.016936 0.022223 0.066074 0.019112
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 1.938303 1.970082 1.977992 1.924757
Std.Err. 0.014143 0.013207 0.012887 0.040712
WINTERELSP leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 1.723757 1.700680 1.743068 1.786364 1.723684 1.799421
Std.Err. 0.057625 0.099113 0.020185 0.024180 0.072426 0.020912
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 1.801200 1.831369 1.828061 1.776699
Std.Err. 0.015604 0.016592 0.018235 0.043706
WINTERWOOD leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 1.944751 1.857143 1.971349 1.946364 1.934211 1.949312
Std.Err. 0.049999 0.096050 0.016018 0.021863 0.065789 0.018868
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 1.952442 1.978241 1.98762 1.929612
Std.Err. 0.013950 0.012938 0.01238 0.040588
WINTERNONE leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 1.248619 1.081633 1.262477 1.130000 1.157895 1.125996
Std.Err. 0.056989 0.094342 0.020246 0.023124 0.069295 0.020023
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 1.128963 1.148685 1.158184 1.101942
Std.Err. 0.014945 0.016216 0.017884 0.041364
NEWC leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. -8.834254 -8.523810 -8.972274 -8.936364 -8.802632 -8.753802
Std.Err. 0.095160 0.176246 0.015993 0.023987 0.113194 0.041715
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. -8.558698 -8.546691 -8.284732 -8.344660
Std.Err. 0.042522 0.062666 0.095642 0.122066
DISH leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 1.591160 1.204082 2.000000e+00 1.000000e+00 1.328947 1.126720
Std.Err. 0.036643 0.033355 2.971530e-16 1.339588e-16 0.038234 0.008955
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 1.080977 1.047144 1.011004 1.004854
Std.Err. 0.005648 0.006385 0.003872 0.003428
WASH leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 1.082873 1.047619 1.073937 1.033636 1.019737 1.018827
Std.Err. 0.020549 0.017625 0.007959 0.005438 0.011319 0.003659
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 1.003856 1.003626 1.004127 1.004854
Std.Err. 0.001283 0.001811 0.002379 0.003428
DRY leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 1.127072 1.047619 1.120148 1.037273 1.046053 1.028240
Std.Err. 0.024824 0.017625 0.009889 0.005714 0.017057 0.004459
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 1.008997 1.005440 1.005502 1.000000e+00
Std.Err. 0.001955 0.002216 0.002745 1.095265e-17
NUNIT2 leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 4.000000e+00 4.000000e+00 1.097967 1.226364 1.026316 1.215062
Std.Err. 2.648036e-16 7.350617e-17 0.012597 0.017651 0.016026 0.014508
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 1.074122 1.031732 1.038514 1.004854
Std.Err. 0.006473 0.006407 0.009018 0.003428
BURNER leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. -5.790055 -5.945578 -5.862292 -5.979091 -6.000000e+00 -5.977552
Std.Err. 0.093039 0.054422 0.031363 0.012084 7.227893e-17 0.011229
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. -5.976864 -5.972801 -5.979367 -6.000000e+00
Std.Err. 0.008748 0.013611 0.014612 8.762122e-17
COOK leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 1.027624 1.006803 1.017560 1.002727 1.000000e+00 1.002896
Std.Err. 0.012216 0.006803 0.003995 0.001573 1.806973e-17 0.001447
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 1.002999 1.003626 1.002751 1.000000e+00
Std.Err. 0.001132 0.001811 0.001944 1.095265e-17
OVEN leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. -5.883978 -5.952381 -5.893715 -5.987273 -6.000000e+00 -5.98407
Std.Err. 0.066612 0.047619 0.026426 0.008995 7.227893e-17 0.00921
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. -5.985004 -5.987307 -5.990371 -6.000000e+00
Std.Err. 0.006701 0.008971 0.009629 8.762122e-17
REFR leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 1.000000e+00 1.013605 1.006470 1.002727 1.013158 1.003621
Std.Err. 6.620091e-17 0.009587 0.002438 0.001573 0.009273 0.001617
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 1.001285 1.000907 1.001376 1.002427
Std.Err. 0.000742 0.000907 0.001376 0.002427
DENS leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.027624 0.183673 0.104436 0.098182 0.151316 0.099203
Std.Err. 0.012216 0.032046 0.009393 0.009068 0.029163 0.008367
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.209940 0.277425 0.350757 0.509709
Std.Err. 0.008877 0.013848 0.019542 0.029858
FAMRM leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.011050 0.074830 0.085028 0.173636 0.217105 0.132513
Std.Err. 0.007792 0.021776 0.008584 0.011712 0.036054 0.009466
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.272065 0.461469 0.500688 0.764563
Std.Err. 0.009737 0.016530 0.022013 0.039197
HALFB leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.165746 0.054422 0.303142 0.595455 0.763158 0.178856
Std.Err. 0.059419 0.018774 0.014578 0.019056 0.051753 0.012225
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.446872 0.818676 0.566713 0.973301
Std.Err. 0.011743 0.016320 0.021079 0.033909
KITCH leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] \
Coef. 1.000000e+00 1.000000e+00 1.000924 1.001818 1.000000e+00
Std.Err. 6.620091e-17 1.837654e-17 0.000924 0.001285 1.806973e-17
leaf[6] leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 1.009413 1.011997 1.016319 1.028886 1.082524
Std.Err. 0.002599 0.002334 0.003817 0.006514 0.013573
LIVING leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] leaf[7] \
Coef. 0.98895 1.061224 1.000000 1.019091 1.052632 1.020999 1.056127
Std.Err. 0.01105 0.022065 0.005231 0.005350 0.020429 0.005722 0.006322
leaf[8] leaf[9] leaf[10]
Coef. 1.068903 1.148556 1.177184
Std.Err. 0.010913 0.017409 0.026405
OTHFN leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.016575 0.034014 0.055453 0.067273 0.144737 0.065170
Std.Err. 0.009516 0.015002 0.007882 0.008581 0.032882 0.007102
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.117823 0.189483 0.229711 0.434466
Std.Err. 0.007815 0.013798 0.021174 0.039427
RECRM leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] leaf[7] \
Coef. 0.0 0.013605 0.023105 0.040909 0.052632 0.030413 0.069837
Std.Err. 0.0 0.009587 0.004569 0.005975 0.018172 0.004623 0.005482
leaf[8] leaf[9] leaf[10]
Coef. 0.153218 0.210454 0.361650
Std.Err. 0.011076 0.015742 0.026522
CLIMB leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 2.308571e+00 2.308571e+00 2.259694 2.216400 2.293383 2.247804
Std.Err. 3.310046e-17 1.102593e-16 0.013614 0.018583 0.015188 0.016434
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 2.286082 2.300894 2.301049 2.308571e+00
Std.Err. 0.004575 0.003673 0.014276 1.971477e-16
ELEV leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. -6.000000e+00 -6.000000e+00 -5.706100 -5.404545 -5.947368 -5.564084
Std.Err. 1.986027e-16 2.940247e-16 0.042939 0.059522 0.052632 0.046176
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. -5.895887 -5.947416 -5.921596 -6.000000e+00
Std.Err. 0.017751 0.018565 0.027616 8.762122e-17
DIRAC leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 1.507923 1.469052 1.475979 1.452383 1.468251 1.452593
Std.Err. 0.012786 0.028698 0.008995 0.010210 0.025063 0.009424
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 1.406490 1.317666 1.283246 1.246568
Std.Err. 0.008602 0.015906 0.021207 0.028282
PORCH leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] leaf[7] \
Coef. 1.149171 1.088435 1.127542 1.077273 1.046053 1.06155 1.048843
Std.Err. 0.026554 0.023498 0.010146 0.008055 0.017057 0.00647 0.004462
leaf[8] leaf[9] leaf[10]
Coef. 1.043518 1.024759 1.021845
Std.Err. 0.006146 0.005767 0.007210
AIRSYS leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 1.397790 1.088435 1.401109 1.201818 1.309211 1.068067
Std.Err. 0.036481 0.023498 0.014907 0.012107 0.037611 0.006780
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 1.064696 1.055304 1.042641 1.038835
Std.Err. 0.005093 0.006885 0.007499 0.009530
WELL leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. -0.696133 -0.564626 -0.866913 -0.908182 -0.960526 -0.908762
Std.Err. 0.054364 0.070323 0.015495 0.012724 0.022639 0.011511
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. -0.871037 -0.844062 -0.887208 -0.808252
Std.Err. 0.010464 0.016306 0.017123 0.029946
WELDUS leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] leaf[7] \
Coef. 4.469613 4.156463 4.720887 4.799091 4.815789 4.816799 4.73479
Std.Err. 0.098342 0.136075 0.031023 0.026495 0.068228 0.022334 0.02060
leaf[8] leaf[9] leaf[10]
Coef. 4.690843 4.768913 4.631068
Std.Err. 0.032063 0.034306 0.056676
STEAM leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.011050 0.081633 -0.054529 -0.079091 0.105263 -0.109341
Std.Err. 0.105697 0.119215 0.042390 0.041720 0.117766 0.036897
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.008997 -0.012693 0.145805 0.031553
Std.Err. 0.029344 0.042464 0.054061 0.070205
OARSYS leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. -1.209945 1.204082 -1.234750 0.340000 -0.500000 1.406951
Std.Err. 0.290425 0.187171 0.118709 0.096368 0.299733 0.054194
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 1.389032 1.395286 1.314993 1.293689
Std.Err. 0.040679 0.055021 0.059886 0.076132
noise1 leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.474392 0.485675 0.491980 0.493226 0.529165 0.496986
Std.Err. 0.020866 0.024247 0.008563 0.008569 0.023549 0.007735
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.506801 0.503722 0.485235 0.532615
Std.Err. 0.005969 0.008567 0.010803 0.013891
noise2 leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.499365 0.477223 0.491978 0.493990 0.505021 0.509057
Std.Err. 0.020791 0.024888 0.008665 0.008633 0.022857 0.007600
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.494212 0.517874 0.508010 0.531369
Std.Err. 0.005963 0.008677 0.010643 0.014090
noise3 leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.485311 0.512201 0.504588 0.498832 0.496952 0.496812
Std.Err. 0.021615 0.022380 0.008794 0.008724 0.023092 0.007969
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.502202 0.506226 0.501597 0.484022
Std.Err. 0.005953 0.008489 0.010746 0.014592
noise4 leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.504756 0.499641 0.479744 0.499257 0.471399 0.495866
Std.Err. 0.021311 0.023497 0.008583 0.008814 0.024742 0.007789
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.493827 0.498341 0.496005 0.495855
Std.Err. 0.005917 0.008545 0.010453 0.014358
noise5 leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.491256 0.513972 0.493933 0.496906 0.466841 0.506005
Std.Err. 0.021763 0.024659 0.008503 0.008690 0.022607 0.007937
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.497487 0.501580 0.506217 0.523169
Std.Err. 0.006008 0.008698 0.010760 0.014213
noise6 leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.491718 0.469613 0.496021 0.498028 0.553031 0.500049
Std.Err. 0.020967 0.024782 0.008862 0.008590 0.022138 0.007662
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.502105 0.514641 0.498158 0.520025
Std.Err. 0.005976 0.008848 0.010962 0.014162
noise7 leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.488858 0.461354 0.501237 0.494184 0.507918 0.498332
Std.Err. 0.021060 0.025089 0.008807 0.008804 0.023145 0.007686
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.501601 0.499010 0.494277 0.491689
Std.Err. 0.005946 0.008495 0.010849 0.014116
noise8 leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.505197 0.495414 0.509971 0.483280 0.471419 0.500312
Std.Err. 0.021648 0.025133 0.008905 0.008613 0.022984 0.007681
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.498416 0.505052 0.513244 0.498875
Std.Err. 0.005990 0.008730 0.010633 0.014676
noise9 leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.503774 0.505684 0.509193 0.503724 0.495117 0.497724
Std.Err. 0.021368 0.022083 0.008729 0.008895 0.024026 0.007790
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.502499 0.497624 0.482065 0.483302
Std.Err. 0.005911 0.008694 0.010711 0.013752
noise10 leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.493354 0.534488 0.496621 0.501796 0.480764 0.514013
Std.Err. 0.022280 0.023470 0.008870 0.008602 0.023038 0.007875
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.486570 0.501135 0.486868 0.478504
Std.Err. 0.006023 0.008704 0.010525 0.014174
noise11 leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.478240 0.476699 0.492790 0.507017 0.479131 0.489874
Std.Err. 0.021454 0.024575 0.009093 0.008602 0.023431 0.007664
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.507827 0.484728 0.482073 0.519721
Std.Err. 0.005912 0.008692 0.010689 0.014121
noise12 leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.519023 0.493302 0.495664 0.507416 0.492513 0.497138
Std.Err. 0.021533 0.025782 0.008673 0.008740 0.023878 0.007687
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.501768 0.494392 0.505834 0.521542
Std.Err. 0.005992 0.008870 0.011018 0.013904
noise13 leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.446577 0.488432 0.512726 0.503292 0.505169 0.501416
Std.Err. 0.021562 0.024128 0.008722 0.008580 0.022691 0.007791
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.500943 0.490835 0.475812 0.469562
Std.Err. 0.006008 0.008713 0.010934 0.014113
noise14 leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.501246 0.502539 0.481349 0.500402 0.504592 0.488694
Std.Err. 0.021904 0.024281 0.008846 0.008779 0.023489 0.007735
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.496610 0.505539 0.490338 0.508695
Std.Err. 0.006006 0.008917 0.010421 0.014288
noise15 leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.469737 0.494470 0.487038 0.509433 0.506092 0.504696
Std.Err. 0.021478 0.021279 0.008892 0.008622 0.023361 0.007789
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.513881 0.490818 0.507790 0.507370
Std.Err. 0.005998 0.008588 0.011194 0.013814
noise16 leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.524719 0.455748 0.502285 0.489549 0.537517 0.491817
Std.Err. 0.021479 0.024267 0.008788 0.008720 0.023624 0.007640
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.501098 0.502460 0.513953 0.480556
Std.Err. 0.005965 0.008707 0.011100 0.013685
noise17 leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.499257 0.538940 0.505553 0.489215 0.484954 0.500511
Std.Err. 0.021145 0.023288 0.008749 0.008696 0.024676 0.007744
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.496586 0.495329 0.494849 0.488306
Std.Err. 0.006046 0.008622 0.010640 0.014218
noise18 leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.487828 0.501180 0.479001 0.500020 0.554518 0.489017
Std.Err. 0.021457 0.025033 0.008648 0.008765 0.022651 0.007716
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.494694 0.500506 0.499138 0.501016
Std.Err. 0.006032 0.008678 0.010996 0.014382
noise19 leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.492477 0.510517 0.497361 0.498034 0.496796 0.497254
Std.Err. 0.021991 0.022717 0.008947 0.008679 0.022420 0.007749
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.506206 0.489874 0.487258 0.513952
Std.Err. 0.006005 0.008683 0.010829 0.014231
noise20 leaf[1] leaf[2] leaf[3] leaf[4] leaf[5] leaf[6] \
Coef. 0.508315 0.525029 0.492421 0.500168 0.514199 0.515827
Std.Err. 0.021264 0.023527 0.008743 0.008766 0.023021 0.007844
leaf[7] leaf[8] leaf[9] leaf[10]
Coef. 0.505397 0.493414 0.493779 0.501220
Std.Err. 0.005925 0.008682 0.010648 0.014518
Finally, as we did in the linear model case, we can use the same code for an annotated version of the same information. Again, we ordered the rows in decreasing order based on an estimate of the relative variance “explained” by leaf membership: \(Var(E[X_i|L_i]) / Var(X_i)\), where \(L_i\) represents the leaf.
df = pd.DataFrame()
for var_name in covariates:
# Looping over covariate names
# Compute average covariate value per ranking (with correct standard errors)
form2 = var_name + " ~ " + "0" + "+" + "leaf"
ols = smf.ols(formula=form2, data=data1).fit(cov_type = 'HC2').summary2().tables[1].iloc[:, 0:2]
# Retrieve results
toget_index = ols["Coef."]
index = toget_index.index
cova1 = pd.Series(np.repeat(var_name,num_leaves), index = index, name = "covariate")
avg = pd.Series(ols["Coef."], name="avg")
stderr = pd.Series(ols["Std.Err."], name = "stderr")
ranking = pd.Series(np.arange(1,num_leaves+1), index = index, name = "ranking")
scaling = pd.Series(norm.cdf((avg - np.mean(avg))/np.std(avg)), index = index, name = "scaling")
data2 = pd.DataFrame(data=x_test, columns= covariates)
variation1= np.std(avg) / np.std(data2[var_name])
variation = pd.Series(np.repeat(variation1, num_leaves), index = index, name = "variation")
labels = pd.Series(round(avg,2).astype('str') + "\n" + "(" + round(stderr, 3).astype('str') + ")", index = index, name = "labels")
# Tally up results
df1 = pd.DataFrame(data = [cova1, avg, stderr, ranking, scaling, variation, labels]).T
df = df.append(df1)
# a small optional trick to ensure heatmap will be in decreasing order of 'variation'
df = df.sort_values(by = ["variation", "covariate"], ascending = False)
df = df.iloc[0:(8*num_leaves), :]
df1 = df.pivot(index = "covariate", columns = "ranking", values = ["scaling"]).astype(float)
labels = df.pivot(index = "covariate", columns = "ranking", values = ["labels"]).to_numpy()
# plot heatmap
ax = plt.subplots(figsize=(18, 10))
ax = sns.heatmap(df1,
annot=labels,
annot_kws={"size": 12, 'color':"k"},
fmt = '',
cmap = "terrain_r",
linewidths=0,
xticklabels = ranking)
plt.tick_params( axis='y', labelsize=15, length=0, labelrotation=0)
plt.tick_params( axis='x', labelsize=15, length=0, labelrotation=0)
plt.xlabel("Leaf (ordered by prediction, low to high)", fontsize= 15)
plt.ylabel("")
ax.set_title("Average covariate values within leaf", fontsize=18, fontweight = "bold")
Text(0.5, 1.0, 'Average covariate values within leaf')
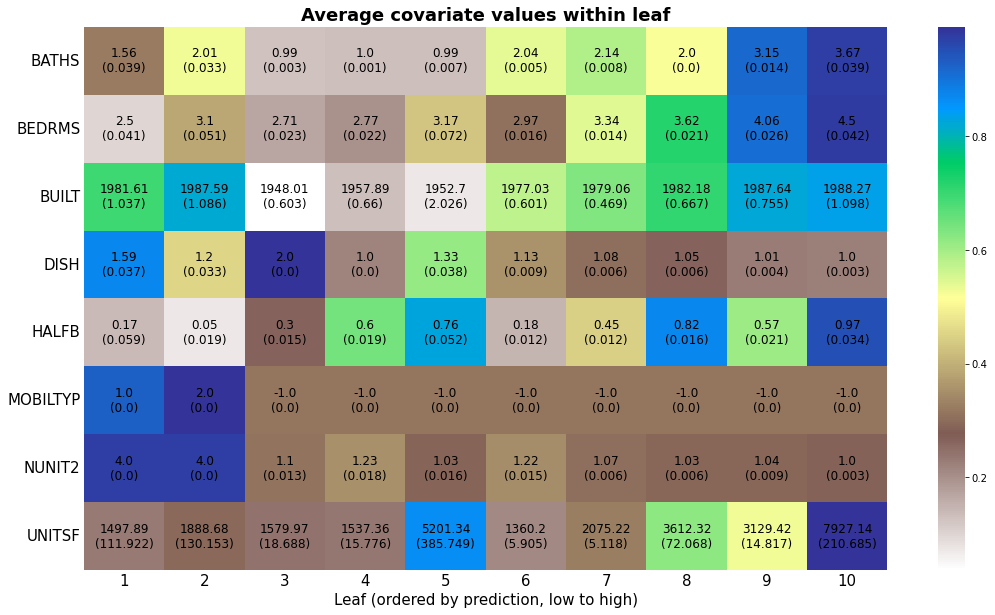
2.2.3. Forest¶
Forests are a type of ensemble estimators: they aggregate information about many decision trees to compute a new estimate that typically has much smaller variance.
At a high level, the process of fitting a (regression) forest consists of fitting many decision trees, each on a different subsample of the data. The forest prediction for a particular point \(x\) is the average of all tree predictions for that point.
One interesting aspect of forests and many other ensemble methods is that cross-validation can be built into the algorithm itself. Since each tree only uses a subset of the data, the remaining subset is effectively a test set for that tree. We call these observations out-of-bag (there were not in the “bag” of training observations). They can be used to evaluate the performance of that tree, and the average of out-of-bag evaluations is evidence of the performance of the forest itself.
For the example below, we’ll use the regression_forest function of the R package grf. The particular forest implementation in grf has interesting properties that are absent from most other packages. For example, trees are build using a certain sample-splitting scheme that ensures that predictions are approximately unbiased and normally distributed for large samples, which in turn allows us to compute valid confidence intervals around those predictions. We’ll have more to say about the importance of these features when we talk about causal estimates in future chapters. See also the grf website for more information.
from sklearn.ensemble import RandomForestRegressor
# Fitting the forest
# We'll use few trees for speed here.
# In a practical application please use a higher number of trees.
forest = RandomForestRegressor(n_estimators=200)
#x_train, x_test, y_train, y_test = train_test_split(XX.to_numpy() , Y, test_size=.3)
forest.fit(x_train, y_train)
# Retrieving forest predictions
y_pred = forest.predict(x_test)
# Evaluation (out-of-bag mse)
mse = mean_squared_error(y_test, y_pred)
print("Forest MSE (out-of-bag):", mse)
Forest MSE (out-of-bag): 0.6516070635940446
The fitted attribute feature_importances_ computes the decrease in node impurity weighted by the probability of reaching that node. The node probability can be calculated by the number of samples that reach the node, divided by the total number of samples. The higher the value the more important the feature.
plt.figure(figsize=(20,10))
sorted_idx = forest.feature_importances_.argsort()[:10]
plt.barh(XX.columns[sorted_idx], forest.feature_importances_[sorted_idx])
plt.tick_params( axis='y', labelsize=15, length=0, labelrotation=0)
plt.tick_params( axis='x', labelsize=15, length=0, labelrotation=0)
plt.title("Random Forest Feature Importance", fontsize = 15, fontweight = "bold")
Text(0.5, 1.0, 'Random Forest Feature Importance')
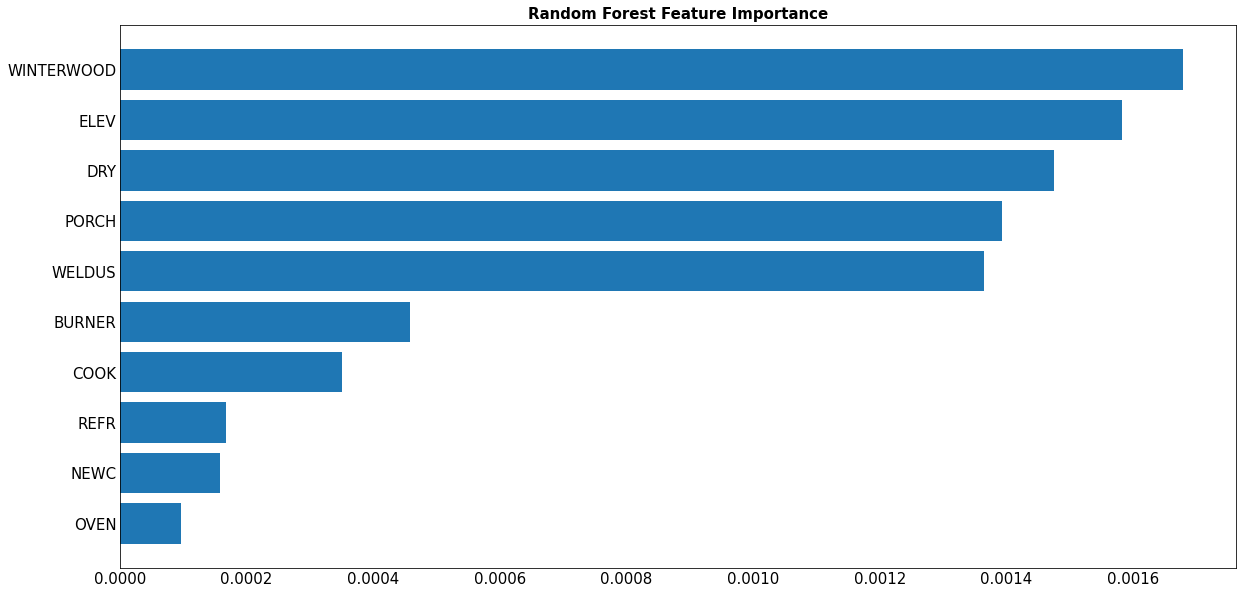
All the caveats about interpretation that we mentioned above apply in a similar to forest output.
2.3. Further reading¶
In this tutorial we briefly reviewed some key concepts that we recur later in this tutorial. For readers who are entirely new to this field or interested in learning about it more depth, the first few chapters of the following textbook are an acccessible introduction:
James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An introduction to statistical learning (Vol. 112, p. 18). New York: springer. Available for free at the authors’ website.
Some of the discussion in the Lasso section in particular was drawn from Mullainathan and Spiess (JEP, 2017), which contains a good discussion of the interpretability issues discussed here.
There has been a good deal of research on inference in high-dimensional models, Although we won’t be covering in depth it in this tutorial, we refer readers to Belloni, Chernozhukov and Hansen (JEP, 2014). Also check out the related R package hdm, developed by the same authors, along with Philipp Bach and Martin Spindler.
